
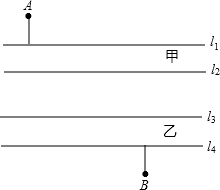
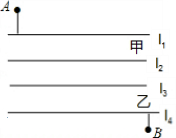
 五羊大学建立分校,校本部与分校隔着两条平行的小河.如图,l1∥l2表示小河甲,l3∥l4表示小河乙,A为校本部大门,B为分校大门.为方便人员来往,要在两条小河上各建一条桥,桥面垂直于河岸.
五羊大学建立分校,校本部与分校隔着两条平行的小河.如图,l1∥l2表示小河甲,l3∥l4表示小河乙,A为校本部大门,B为分校大门.为方便人员来往,要在两条小河上各建一条桥,桥面垂直于河岸. ≈218(米).
≈218(米).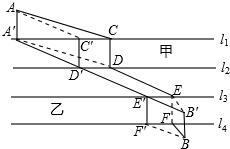


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
 如图,五羊大学建立分校,校本部与分校隔着两条平行的小河,l1∥l2表示小河甲,l3∥l4表示小河乙,A为校本部大门,B为分校大门,为方便人员来往,要在两条小河上各建一座桥,桥面垂直于河岸.图中的尺寸是:甲河宽8米,乙河宽10米,A到甲河垂直距离为40米,B到乙河垂直距离为20米,两河距离100米,A、B两点水平距离(与小河平行方向)120米,为使A、B两点间来往路程最短,两座桥都按这个目标而建,那么,此时A、D两点间来往的路程是多少米?
如图,五羊大学建立分校,校本部与分校隔着两条平行的小河,l1∥l2表示小河甲,l3∥l4表示小河乙,A为校本部大门,B为分校大门,为方便人员来往,要在两条小河上各建一座桥,桥面垂直于河岸.图中的尺寸是:甲河宽8米,乙河宽10米,A到甲河垂直距离为40米,B到乙河垂直距离为20米,两河距离100米,A、B两点水平距离(与小河平行方向)120米,为使A、B两点间来往路程最短,两座桥都按这个目标而建,那么,此时A、D两点间来往的路程是多少米?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com