
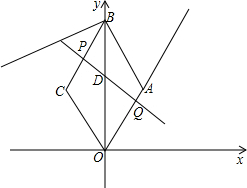
 已知:如图,在平面直角坐标系中,四边形ABCO是菱形,且∠AOC=60°,点B的坐标是(0,8$\sqrt{3}$),点P从点C开始以每秒1个单位长度的速度沿线段CB向点B移动,同时,点Q从点O开始以每秒3个单位长度的速度沿射线OA方向移动,点P运动到点B时,两点停止运动.直线PQ交OB于点D,运动时间为t秒.
已知:如图,在平面直角坐标系中,四边形ABCO是菱形,且∠AOC=60°,点B的坐标是(0,8$\sqrt{3}$),点P从点C开始以每秒1个单位长度的速度沿线段CB向点B移动,同时,点Q从点O开始以每秒3个单位长度的速度沿射线OA方向移动,点P运动到点B时,两点停止运动.直线PQ交OB于点D,运动时间为t秒.分析 (1)连接AC交OB于点M,根据菱形的性质,在RT△AMO中,求出AM、OM即可.
(2)分两种情形①如图1中,当PQ⊥OA时,过C作CH⊥OA于H,②如图2中,当PQ⊥AB时,过P作PN∥AB交射线OA于N,分别利用直角三角形30度性质列出方程即可解决.
(3)当a=1,a=3时,以O,Q,D为顶点的三角形与△OAB相似,①当a=1,△ODQ∽△OBA,②a=3时,△ODQ∽△OAB分别根据相似三角形性质列出方程即可解决.
解答 解:(1)连接AC交OB于点M,
∵∠AOC=60°,四边形ABCO是菱形,
∴AC垂直平分OB,OM=$\frac{1}{2}$OB=4$\sqrt{3}$,∠AOM=30°,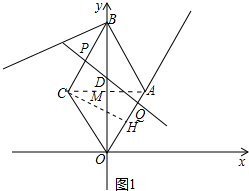
∴AM=4,
∴点D坐标为A(4,$4\sqrt{3}$).
(2)①如图1中,当PQ⊥OA时,过C作CH⊥OA于H,
∵PQ∥CH,PC∥QH,
∴四边形PCHQ是平行四边形,
∵∠CHQ=90°,
∴四边形PCHQ是矩形,
∴PC=QH=t,OQ=3t,∠OCH=30°,OH=2t=$\frac{1}{2}OC=4$,
∴t=2.
②如图2中,当PQ⊥AB时,过P作PN∥AB交射线OA于N,
由菱形ABCO得,PN=AB=8,
∴OQ=3t,CP=t,∠PQN=30°,NQ=2t=16,
∴t=8,
即当t=2,t=8时,直线PQ与菱形ABCO的边互相垂直.
(3)当a=1,a=3时,以O,Q,D为顶点的三角形与△OAB相似,
①当a=1,△ODQ∽△OBA,
证明:由△ODQ∽△OBA,可得∠ODQ=∠OBA,此时PQ∥AB,
∴四边形PCOQ为平行四边形,
∴CP=OQ,即at=t,(0<t≤8)
∴a=1时,△ODQ∽△OBA,
②a=3时,△ODQ∽△OAB
当P与B重合时,D点也与B重合,此时t=8,
由△ODQ∽△OAB,得$\frac{OD}{OA}=\frac{OQ}{OB}$,
∵OD=OB,
∴OB2=OA•OQ,
即$(8\sqrt{3}{)^2}=8×8a$,
∴a=3,
∴a=3,△ODQ∽△OAB.
点评 本题考查相似三角形的判定和性质、菱形的判定和性质、直角三角形30度的性质等知识,解题的关键是学会分类讨论,正确画出图形,把问题转化为方程去解决,属于中考压轴题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com