
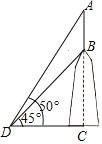
【题目】如图,建筑物BC的屋顶有一根旗杆AB,从地面上点D处观测旗杆顶点A的仰角为50°,观测旗杆底部点B的仰角为45°.若旗杆的高度AB为3.5米,则建筑物BC的高度约为_____米.(精确到1米,可用参考数据:sin50°≈0.8,tan50°≈1.2)
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知y关于x的二次函数y=x-bx+![]() b+b-5的图象与x轴有两个公共点.
b+b-5的图象与x轴有两个公共点.
(1)求b的取值范围;
(2)若b取满足条件的最大整数值,当m≤x≤![]() 时,函数y的取值范围是n≤y≤6-2m,求m,n的值;
时,函数y的取值范围是n≤y≤6-2m,求m,n的值;
(3)若在自变量x的值满足b≤x≤b+3的情况下,对应函数y的最小值为![]() ,求此时二次函数的解析式.
,求此时二次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
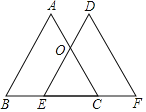
【题目】如图,在△ABC中,AB=AC.将△ABC沿着BC方向平移得到△DEF,其中点E在边BC上,DE与AC相交于点O.连接AE、DC、AD,当点E在什么位置时,四边形AECD为矩形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C为⊙O上一点,AD⊥CD,(点D在⊙O外)AC平分∠BAD.

(1)求证:CD是⊙O的切线;
(2)若DC、AB的延长线相交于点E,且DE=12,AD=9,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
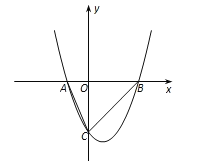
【题目】如图,已知二次函数y=x2-mx-m-1的图像交x轴于A、B两点(A、B分别位于坐标原点O的左、右两侧),交y轴于点C,且△ABC的面积为6.
(1)求这个二次函数的表达式;
(2)若P为平面内一点,且PB=3PA,试求当△PAB的面积取得最大值时点P的坐标,并求此时直线PO将△ABC分成的两部分的面积之比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[问题]小明在学习时遇到这样一个问题:求不等式x3+3x2﹣x﹣3>0的解集.
他经历了如下思考过程:
[回顾]
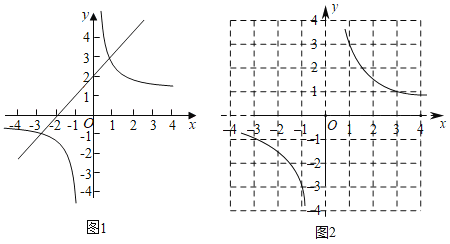
(1)如图1,在平面直角坐标系xOy中,直线y1=ax+b与双曲线y2=![]() 交于A (1,3)和B(﹣3,﹣1),则不等式ax+b>
交于A (1,3)和B(﹣3,﹣1),则不等式ax+b>![]() 的解集是 .
的解集是 .
[探究]将不等式x3+3x2﹣x﹣3>0按条件进行转化:
当x=0时,原不等式不成立;
当x>0时,不等式两边同除以x并移项转化为x2+3x﹣1>![]() ;
;
当x<0时,不等式两边同除以x并移项转化为x2+3x﹣1<![]() .
.
(2)构造函数,画出图象:
设y3=x2+3x﹣1,y4=![]() ,在同一坐标系中分别画出这两个函数的图象;
,在同一坐标系中分别画出这两个函数的图象;
双曲线y4=![]() 如图2所示,请在此坐标系中画出抛物线y=x2+3x﹣1.(不用列表)
如图2所示,请在此坐标系中画出抛物线y=x2+3x﹣1.(不用列表)
(3)确定两个函数图象公共点的横坐标:
观察所画两个函数的图象,猜想并通过代入函数解析式验证可知:满足y3=y4的所有x的值为 .
[解决]
(4)借助图象,写出解集:
结合“探究”中的讨论,观察两个函数的图象可知:不等式x3+3x2﹣x﹣3>0的解集为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《孙子算经》是中国古代重要的数学著作,其中记载:“今有甲、乙二人,持钱各不知数.甲得乙中半,可满四十八;乙得甲太半,亦满四十八。问甲、乙二人原持钱各几何?”译文:“甲,乙两人各有若干钱,如果甲得到乙所有钱的一半,那么甲共有钱48文,如果乙得到甲所有钱的![]() ,那么乙也共有钱48文,问甲、乙二人原来各有多少钱?”
,那么乙也共有钱48文,问甲、乙二人原来各有多少钱?”
查看答案和解析>>
科目:初中数学 来源: 题型:
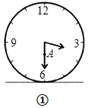
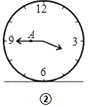
【题目】图①表示一个时钟的钟面垂直固定于水平桌面上,其中分针上有一点![]() ,当钟面显示3点30分时,分针垂直于桌面,点
,当钟面显示3点30分时,分针垂直于桌面,点![]() 距离桌面的高度为
距离桌面的高度为![]() 公分,图②表示钟面显示3点45时,点
公分,图②表示钟面显示3点45时,点![]() 距桌面的高度为
距桌面的高度为![]() 公分,若钟面显示3点55时,点
公分,若钟面显示3点55时,点![]() 距离桌面的高度为__________公分.
距离桌面的高度为__________公分.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com