
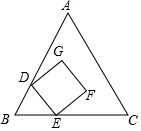
 如图为等边三角形ABC与正方形DEFG的重叠情形,其中D、E两点分别在AB,BC上,且BD=BE,若AC=19,GF=6,则点F到AC的距离为$\frac{13}{2}$$\sqrt{3}$-6.
如图为等边三角形ABC与正方形DEFG的重叠情形,其中D、E两点分别在AB,BC上,且BD=BE,若AC=19,GF=6,则点F到AC的距离为$\frac{13}{2}$$\sqrt{3}$-6. 分析 过点B作BH⊥AC于H,交GF于K,根据等边三角形的性质求出∠A=∠ABC=60°,然后判定△BDE是等边三角形,再根据等边三角形的性质求出∠BDE=60°,然后根据同位角相等,两直线平行求出AC∥DE,再根据正方形的对边平行得到DE∥GF,从而求出AC∥DE∥GF,再根据等边三角形的边与高的关系表示出KH,然后根据平行线间的距离相等即可得解.
解答  解:如图,过点B作BH⊥AC于H,交GF于K,
解:如图,过点B作BH⊥AC于H,交GF于K,
∵△ABC是等边三角形,
∴∠A=∠ABC=60°,
∵BD=BE,
∴△BDE是等边三角形,
∴∠BDE=60°,
∴∠A=∠BDE,
∴AC∥DE,
∵四边形DEFG是正方形,GF=6,
∴DE∥GF,
∴AC∥DE∥GF,
∴KH=19×$\frac{\sqrt{3}}{2}$-6×$\frac{\sqrt{3}}{2}$-6=$\frac{13}{2}$$\sqrt{3}$-6,
∴F点到AC的距离为$\frac{13}{2}$$\sqrt{3}$-6.
故答案为:$\frac{13}{2}$$\sqrt{3}$-6.
点评 本题考查了正方形的对边平行,四条边都相等的性质,等边三角形的判定与性质,等边三角形的高线等于边长的$\frac{\sqrt{3}}{2}$倍,以及平行线间的距离相等的性质,综合题,但难度不大,熟记各图形的性质是解题的关键.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:初中数学 来源:2016-2017学年福建省仙游县郊尾、枫亭五校教研小片区七年级下学期第一次月考数学试卷(解析版) 题型:单选题
已知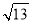 ≈3.606,
≈3.606, 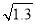 ≈1.140,根据以上信息可求得
≈1.140,根据以上信息可求得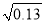 的近似值是(结果精确到0.01)( )
的近似值是(结果精确到0.01)( )
A. 36.06 B. 0.36 C. 11.40 D. 0.11
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=-x | B. | y=3-2x | C. | y=$\frac{1}{x}$(x>0) | D. | y=x2(x>0) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
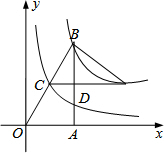 如图,Rt△ABO中,∠OAB=Rt∠,点A在x轴的正半轴,点B在第一象限,C,D分别是BO,BA的中点,点E在CD的延长线上.若函数y1=$\frac{{k}_{1}}{x}$(x>0)的图象经过B,E,函数y2=$\frac{{k}_{2}}{x}$ (x>0)的图象过点C,且△BCE的面积为1,则k2的值为( )
如图,Rt△ABO中,∠OAB=Rt∠,点A在x轴的正半轴,点B在第一象限,C,D分别是BO,BA的中点,点E在CD的延长线上.若函数y1=$\frac{{k}_{1}}{x}$(x>0)的图象经过B,E,函数y2=$\frac{{k}_{2}}{x}$ (x>0)的图象过点C,且△BCE的面积为1,则k2的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | 3 | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com