练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7、已知一个正多边形的内角和是540°，则这个正多边形的一个外角是（　　）
    分析：根据多边形的内角和公式（n-2）•180°求出多边形的边数，再根据多边形的外角和是固定的360°，依此可以求出多边形的一个外角．
    解答：解：∵正多边形的内角和是540°，
    ∴多边形的边数为540°÷180°+2=5，
    ∵多边形的外角和都是360°，
    ∴多边形的每个外角=360÷5=72°．
    故选C．
    点评：本题主要考查了多边形的内角和与外角和之间的关系，关键是记住内角和的公式与外角和的特征，难度适中．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    归纳猜想：同学们，让我们一起进行一次研究性学习：
    （1）如图1已知正三角形ABC的中心为O，半径为R，将其沿直线l向右翻滚，当正三角形翻滚一周时，其中心O经过的路程是多少？

    （2）如图2将半径为R的正方形沿直线l向右翻滚，当正方形翻滚一周时，其中心O经过的路程是多少？

    （3）猜想：把正多边形翻滚一周，其中心O所经过的路程是多少（R为正多边形的半径，可参看图2）？请说明理由．

    （4）进一步猜想：任何多边形都有一个外接圆，若将任意圆内接多边形翻滚一周时，其外心所经过的路程是否是一个定值（R为多边形外接圆的半径）？为什么？请以任意三角形为例说明（如图12）．
    通过以上猜想你可得到什么样的结论？请写出来．

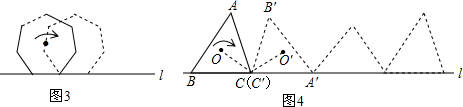
    查看答案和解析>>

    科目：初中数学 来源： 题型：044

    已知一个圆的半径为R．

    (1)求这个圆的内接正n边形的周长和面积；

    (2)利用(1)的结果填写下表：

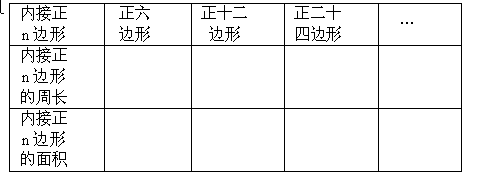
    观察上表，随着圆内接正多边形边数的增加，正多边形的周长(面积)有怎样的变化趋势，与圆的周长(面积)进行比较，你能得出什么结论？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    归纳猜想：同学们，让我们一起进行一次研究性学习：
    （1）如图1已知正三角形ABC的中心为O，半径为R，将其沿直线l向右翻滚，当正三角形翻滚一周时，其中心O经过的路程是多少？

    （2）如图2将半径为R的正方形沿直线l向右翻滚，当正方形翻滚一周时，其中心O经过的路程是多少？

    （3）猜想：把正多边形翻滚一周，其中心O所经过的路程是多少（R为正多边形的半径，可参看图2）？请说明理由．

    （4）进一步猜想：任何多边形都有一个外接圆，若将任意圆内接多边形翻滚一周时，其外心所经过的路程是否是一个定值（R为多边形外接圆的半径）？为什么？请以任意三角形为例说明（如图12）．
    通过以上猜想你可得到什么样的结论？请写出来．

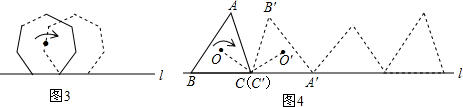
    查看答案和解析>>

    科目：初中数学 来源：2009年第7届“学用杯”全国数学知识应用竞赛九年级初赛试卷（A卷）（解析版） 题型：解答题

    归纳猜想：同学们，让我们一起进行一次研究性学习：
    （1）如图1已知正三角形ABC的中心为O，半径为R，将其沿直线l向右翻滚，当正三角形翻滚一周时，其中心O经过的路程是多少？

    （2）如图2将半径为R的正方形沿直线l向右翻滚，当正方形翻滚一周时，其中心O经过的路程是多少？

    （3）猜想：把正多边形翻滚一周，其中心O所经过的路程是多少（R为正多边形的半径，可参看图2）？请说明理由．

    （4）进一步猜想：任何多边形都有一个外接圆，若将任意圆内接多边形翻滚一周时，其外心所经过的路程是否是一个定值（R为多边形外接圆的半径）？为什么？请以任意三角形为例说明（如图12）．
    通过以上猜想你可得到什么样的结论？请写出来．

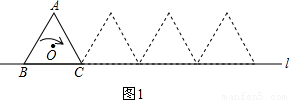
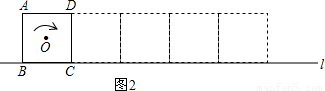
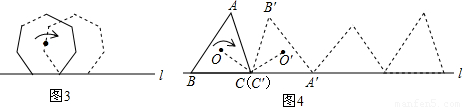
    查看答案和解析>>

    同步练习册答案