练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    19．若正数m的两个平方根分别是a+2与3a-6，则m的值为9．

    分析 直接利用平方根的定义得出a的值，进而得出m的值．

    解答 解：∵正数m的两个平方根分别是a+2与3a-6，
    ∴a+2+3a-6=0，
    解得：a=1，
    则a+2=3，
    则m的值为：9，
    故答案为：9．

    点评 此题主要考查了平方根，正确利用平方根的定义得出a的值是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    9．某汽车专卖店销售A，B两种型号的新能源汽车，购进1辆A型车和3辆B型车进价为81万元；购进2辆A型车和1辆B型车进价为52万元．
    （1）求每辆A型车和B型车的进价各为多少元．
    （2）该汽车专卖店拟向厂家采购A，B两种型号的新能源汽车共6辆，购车费不少于97万元，且不超过104万元．则有哪几种购车方案？
    （3）一辆A型车售价18万元，一辆B型车售价26万元，在（2）的条件下汽车专卖店要想获得最大利润应选择哪种采购方案，此时最大利润是多少万元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．阅读下列材料：求不等式（2x-1）（x+3）＞0的解集．
    解：根据“同号两数相乘，积为正”可得：①$\left\{\begin{array}{l}2x-1＞0\\ x+3＞0\end{array}\right.$或 ②$\left\{\begin{array}{l}2x-1＜0\\ x+3＜0\end{array}\right.$．
    解①得x＞$\frac{1}{2}$；  解②得x＜-3．
    ∴不等式的解集为x＞$\frac{1}{2}$或x＜-3．
    请你仿照上述方法解决问题：求不等式（2x-3）（x+1）＜0的解集．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．若x2-2x-5=0的一个解为a，则a（2a-3）+a（1-a）的值为（　　）
    A．$\sqrt{6}$B．2$\sqrt{6}$+4C．5D．-5

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．2015年12月19日郑州机场T2航站楼正式启用，为了宣传T2航站楼，机场反面要印刷一批宣传材料，经招标，某印务公司中标，该印务公司提出3种方案：
    方案一：每份材料收印刷费1元；
    方案二：收制版费1000元，另外每份材料收印刷费m元；
    方案三：印数在1000份以内时，每份材料收印刷费1.2元，超过1000份时超过部分按每份n元收取．
    （1）若机场方面选用方案二和方案三各印刷2000份材料需花费3900元，选用方案二和方案三各印刷3000份材料需花费5100元，请求出m和n的值；
    （2）分别写出各方案的收费y（元）与印刷材料的份数x（份）之间的函数关系式；
    （3）若机场方面预计要印刷5000份以内的宣传材料，请根据图象求出A、B、C的坐标，并直接写出机场方面应选择哪一种方案更合算？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．已知a是实数$\sqrt{10}$的整数部分，b是$\sqrt{10}$的小数部分，那么a-b值是（　　）
    A．3+$\sqrt{10}$B．3-$\sqrt{10}$C．$\sqrt{10}$-3D．6-$\sqrt{10}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

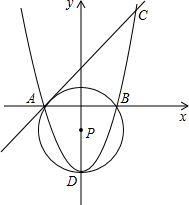    11．在平面直角坐标系中，已知点A（-2，0），B（2，0），C（3，5）．
    （1）求过点A，C的直线解析式和过点A，B，C的抛物线的解析式；
    （2）求过点A，B及抛物线的顶点D的⊙P的圆心P的坐标；
    （3）在抛物线上是否存在点Q，使AQ与⊙P相切，若存在请求出Q点坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．解不等式：$\frac{2x-3}{3}-\frac{3x-2}{2}＞\frac{5}{6}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

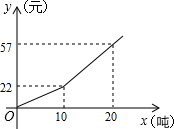    20．为了节约水资源，自来水公司按分段收费标准收费，如图所示反映的是每月收取水费y（元）与用水量x（吨）之间的函数关系，当每月用水量14吨时，水费是36元．

    查看答案和解析>>

    同步练习册答案