
【题目】如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.
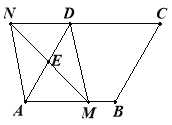
(1)求证:四边形AMDN是平行四边形;
(2)填空:①当AM的值为 时,四边形AMDN是矩形;②当AM的值为 时,四边形AMDN是菱形。
【答案】(1)、证明过程见解析;(2)、①、1;②、2.
【解析】
试题分析:(1)、根据菱形的性质得到NC∥AB,说明∠DNE=∠AME,根据中点得出DE=AE,结合对顶角得出△NDE≌△MAE,从而说明ND=AM,根据一组对边平行且相等的四边形为平行四边形进行判断;(2)、根据矩形和菱形的性质进行说明.
试题解析:(1)、∵ABCD为菱形 ∴NC∥AB ∴∠DNE=∠AME ∵E为AD的中点 ∴DE=AE
又∵∠NED=∠MEA ∴△NDE≌△MAE ∴ND=AM ∵ND∥AM ∴四边形AMDN为平行四边形
(2)、①、当四边形AMDN为矩形时,则DM⊥AB ∵∠DAB=60° ∴△DAB为正三角形
∴点M为AB的中点 ∴AM=1
②、当四边形AMDN为菱形使,则AM=AD=2.


科目:初中数学 来源: 题型:
【题目】为支持地方,大庆市萨尔图区、让胡路区、红岗区三地现分别有物资100吨、100吨、80吨,需全部运往肇东和肇源两地,根据需要情况,这批物资运往肇东的数量比运往肇源的数量的2倍少20吨。
(1)求这赈灾物资运往肇东和肇源的数量各是多少?
(2)若要求红岗区运往肇东的物资为60吨,萨尔图区地运往肇东的物资为![]() 吨(
吨(![]() 为整数),让胡路区运往肇东的物资数量小于萨尔图区地运往肇东的物资数量的2倍,其余的物资全部运往肇源,且让胡路区运往肇源的物资数量不超过25吨,则萨尔图区、让胡路区两地的物资运往肇东和肇源的方案有几种?
为整数),让胡路区运往肇东的物资数量小于萨尔图区地运往肇东的物资数量的2倍,其余的物资全部运往肇源,且让胡路区运往肇源的物资数量不超过25吨,则萨尔图区、让胡路区两地的物资运往肇东和肇源的方案有几种?
(3)已知萨尔图区、让胡路区、红岗区三地的物资运往肇东和肇源的费用如下表:
萨尔图区 | 让葫芦区 | 红岗区 | |
运往肇东的费用(元/吨) | 220 | 200 | 200 |
运往肇源的费用(元/吨) | 250 | 220 | 210 |
为即时将这批物资运往肇东和肇源,某公司主动承担运送这批物资的总费用,在(2)问的要求下,该公司承担运送这批物资的总费用最多是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,对角线AC与BD相交于点O,AE⊥BD于E,若BE:ED=1:3,AD=6. (1)求∠BAE的度数;(2)求AE的长.
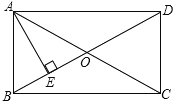
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】江苏卫视《最强大脑》曾播出一期“辨脸识人”节目,参赛选手以家庭为单位,每组家庭由爸爸妈妈和宝宝3人组成,爸爸、妈妈和宝宝分散在三块区域,选手需在宝宝中选一个宝宝,然后分别在爸爸区域和妈妈区域中正确找出这个宝宝的父母,不考虑其他因素,仅从数学角度思考,已知在本期比赛中有A、B、C三组家庭进行比赛.
(1)若机器人智能小度选择A组家庭的宝宝,求小度在妈妈区域中正确找出其妈妈的概率;
(2)如果任选一个宝宝(假如选A组家庭),通过列表或树状图的方法,求机器人智能小度至少正确找对宝宝父母其中一人的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】去年以来,我国中东部地区持续出现雾霾天气.我市某记者为了了解“雾霾天气的主要成因”,随机调查了部分市民,并对调查结果进行整理,绘制了如下尚不完整的统计表:
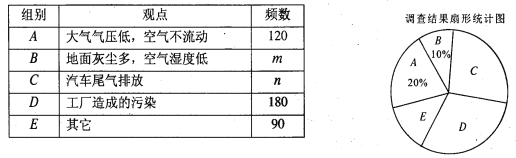
请根据图表中提供的信息解答下列问题:
(1)填空:m= ,n= ,扇形统计图中E组所占的百分比为 ;
(2)若该市人口约有75万人,请你估计其中持D组“观点”的市民人数;
(3)若在这次接受调查的市民中,随机抽查一人,则此人持C组“观点”的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,若直线y=ax-b经过第一、二、三象限,则直线y=bx-a不经过的象限是
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com