
【题目】我们规定:若关于![]() 的一元一次方程
的一元一次方程![]() 的解为
的解为![]() ,则称该方程为“和解方程”.例如:方程
,则称该方程为“和解方程”.例如:方程![]() 的解为
的解为![]() ,而
,而![]() , 则方程
, 则方程![]() 为“和解方程".请根据上述规定解答下列问题:(1)已知关于
为“和解方程".请根据上述规定解答下列问题:(1)已知关于![]() 的一元一次方程
的一元一次方程![]() 是“和解方程”,则
是“和解方程”,则![]() 的值为________.(2)己知关于
的值为________.(2)己知关于![]() 的一元一次方程
的一元一次方程![]() 是“和解方程”,并且它的解是
是“和解方程”,并且它的解是![]() ,则
,则![]() 的值为_________.
的值为_________.
科目:初中数学 来源: 题型:
【题目】某校七年级学生在农场进行社会实践劳动时,采摘了黄瓜和茄子共![]() 千克,了解到采摘的这部分黄瓜和茄子的种植成本共
千克,了解到采摘的这部分黄瓜和茄子的种植成本共![]() 元,还了解到如下信息:黄瓜的种植成本是
元,还了解到如下信息:黄瓜的种植成本是![]() 元/千克,售价是
元/千克,售价是![]() 元/千克;茄子的种植成本是
元/千克;茄子的种植成本是![]() 元/千克,售价是
元/千克,售价是![]() 元/千克.
元/千克.
(1)求采摘的黄瓜和茄子各多少千克?
(2)这些采摘的黄瓜和茄子全部卖出可赚多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上A,B两点对应的有理数分别为10和15,点P从点A出发,以每秒1个单位长度的速度沿数轴正方向运动,点Q同时从原点O出发,以每秒2个单位长度的速度沿数轴正方向运动,设运动时间为t秒.
![]()
(1)当0<t<5时,用含t的式子填空:
BP=_______,AQ=_______;
(2)当t=2时,求PQ的值;
(3)当PQ=![]() AB时,求t的值.
AB时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,点O是AC边上一点,连接BO,交AD于点F,OE⊥OB交BC于点E.
(1)如图1,当O为边AC中点,![]() 时,求
时,求![]() 的值.小明这样想的,过O点作OH∥AB交BC于点H,可证△AOF∽△HOE,于是求出答案,请你直接写出答案
的值.小明这样想的,过O点作OH∥AB交BC于点H,可证△AOF∽△HOE,于是求出答案,请你直接写出答案![]() ;
;
(2)如图2,当O为边AC中点,![]() 时,请求出
时,请求出![]() 的值,并说明理由;
的值,并说明理由;
(3)如图3,当![]() ,
,![]() 时,请直接写出
时,请直接写出![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示是长方体的平面展开图,设![]() ,若
,若![]() .
.
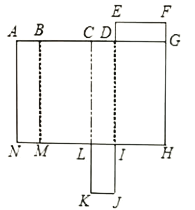
(1)求长方形![]() 的周长与长方形
的周长与长方形![]() 的周长(用字母
的周长(用字母![]() 进行表示) ;
进行表示) ;
(2)若长方形![]() 的周长比长方形
的周长比长方形![]() 的周长少8,求原长方体的体积.
的周长少8,求原长方体的体积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下是通过折叠正方形纸片得到等边三角形的步骤取一张正方形的纸片进行折叠,具体操作过程如下:
第一步:如图,先把正方形ABCD对折,折痕为MN;
第二步:点E在线段MD上,将△ECD沿EC翻折,点D恰好落在MN上,记为点P,连接BP可得△BCP是等边三角形
问题:在折叠过程中,可以得到PB=PC;依据是________________________.
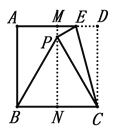
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的一元二次方程ax2+bx﹣1=0(a≠0)有一根为x=2019,则一元二次方程a(x﹣1)2+b(x﹣1)=1必有一根为( )
A.![]() B.2020C.2019D.2018
B.2020C.2019D.2018
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,老师出示了这样一道题目:“当![]() 时,求多项式
时,求多项式![]() 的值”.解完这道题后,张恒同学指出:“
的值”.解完这道题后,张恒同学指出:“![]() 是多余的条件”师生讨论后,一致认为这种说法是正确的,老师及时给予表扬,同学们对张恒同学敢于提出自己的见解投去了赞赏的目光.
是多余的条件”师生讨论后,一致认为这种说法是正确的,老师及时给予表扬,同学们对张恒同学敢于提出自己的见解投去了赞赏的目光.
(1)请你说明正确的理由;
(2)受此启发,老师又出示了一道题目,“无论![]() 取任何值,多项式
取任何值,多项式![]() 的值都不变,求系数
的值都不变,求系数![]() 、
、![]() 的值”.请你解决这个问题.
的值”.请你解决这个问题.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com