
操作与探究
我们知道:过任意一个三角形的三个顶点能作一个圆,探究过四边形四个顶点作圆的条件。
(1)分别测量下面各四边形的内角,如果过某个四边形的四个顶点能一个圆,那么其相对的两个角之间有什么关系?证明你的发现.

(2) 如果过某个四边形的四个顶点不能一个圆,那么其相对的两个角之间有上面的关系吗?试结合下面的两个图说明其中的道理.(提示:考虑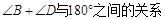 )
)

由上面的探究,试归纳出判定过四边形的四个顶点能作一个圆的条件.
(1)对角互补(对角之和等于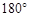 );(2) 图1中,
);(2) 图1中,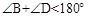 ;图2中,
;图2中,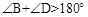 ;
;
过四边形的四个顶点能作一个圆的条件是:对角互补(对角之和等于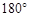 ).
).
【解析】
试题分析:(1)通过测量,过某个四边形的四个顶点能一个圆,那么其相对的两个角之和等于180°.
(2) 如果过某个四边形的四个顶点不能一个圆,那么其相对的两个角之间没有上面的关系,要么相对两角之和大于180°,如图2,要么两角之和小于180°如图1.总之,过四边形的四个顶点能作一个圆的条件是:对角互补(对角之和等于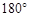 )
)
试题解析:(1)对角互补(对角之和等于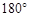 )
)
(2) 图1中,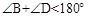
图2中,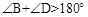
过四边形的四个顶点能作一个圆的条件是:对角互补(对角之和等于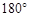 )
)
考点: 圆的内切四边形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
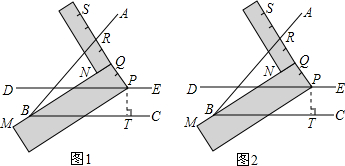 (1)阅读理解:
(1)阅读理解: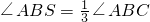 是否成立?如果成立,请说明理由;如果不成立,请在图2中∠ABC的外部画出
是否成立?如果成立,请说明理由;如果不成立,请在图2中∠ABC的外部画出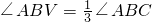 (无需写画法,保留画图痕迹即可).
(无需写画法,保留画图痕迹即可).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com