
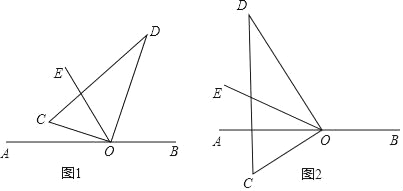
【题目】如图,直角三角板的直角顶点O在直线AB上,OC,OD是三角板的两条直角边,OE平分∠AOD.
(1)若∠COE=20°,则∠BOD= ;若∠COE=α,则∠BOD= (用含α的代数式表示)
(2)当三角板绕O逆时针旋转到图2的位置时,其它条件不变,试猜测∠COE与∠BOD之间有怎样的数量关系?并说明理由.
【答案】(1)40°;2α;(2)∠BOD=2∠COE.
【解析】试题分析:(1)先根据直角计算∠DOE的度数,再同角平分线的定义计算∠AOD的度数,最后利用平角的定义可得结论;
(2)设∠BOD=β,则∠AOD=180°-β,根据角平分线的定义表示∠BOE,再利用互余的关系求∠COE的度数,可得结论.
试题解析:(1)若∠COE=20°,
∵∠COD=90°,
∴∠EOD=90°﹣20°=70°,
∵OE平分∠AOD,
∴∠AOD=2∠EOD=140°,
∴∠BOD=180°﹣140°=40°;
若∠COE=α,
∴∠EOD=90﹣α,
∵OE平分∠AOD,
∴∠AOD=2∠EOD=2(90﹣α)=180﹣2α,
∴∠BOD=180°﹣(180﹣2α)=2α;
故答案为:40°;2α;
(2)如图2,∠BOD=2∠COE,理由是:
设∠BOD=β,则∠AOD=180°﹣β,
∵OE平分∠AOD,
∴∠EOD=![]() ∠AOD=
∠AOD=![]() =90°﹣
=90°﹣![]() ,
,
∵∠COD=90°,
∴∠COE=90°﹣(90°﹣![]() )=
)=![]() ,
,
即∠BOD=2∠COE.


科目:初中数学 来源: 题型:
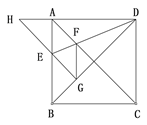
【题目】如图,正方形ABCD的边长为1,AC,BD是对角线。将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG。则下列结论:
①四边形AEGF是菱形 ②△AED≌△GED
③∠DFG=112.5° ④BC+FG=1.5
其中正确的结论是( )
A. ①②③④ B. ①②③ C. ①② D. ②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(0,2),△AOB为等边三角形,P是x轴上一个动点(不与原O重合),以线段AP为一边在其右侧作等边三角形△APQ.

(1)求点B的坐标;
(2)在点P的运动过程中,∠ABQ的大小是否发生改变?如不改变,求出其大小;如改变,请说明理由.
(3)连接OQ,当OQ∥AB时,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△A1C1C2的周长为1,作C1D1⊥A1C2于D1,在C1C2的延长线上取点C3,使D1C3=D1C1,连接D1C3,以C2C3为边作等边△A2C2C3;作C2D2⊥A2C3于D2,在C2C3的延长线上取点C4,使D2C4=D2C2,连接D2C4,以C3C4为边作等边△A3C3C4;…且点A1,A2,A3,…都在直线C1C2同侧,如此下去,则△A1C1C2,△A2C2C3,△A3C3C4,…,△AnCnCn+1的周长和为______.(n≥2,且n为整数)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)观察思考
如图所示,线段AB上的点数与线段的总条数有如下关系:如果线段AB上有3个点,那么线段总条数为3;如果线段AB上有4个点,那么线段总条数为6;如果线段AB上有5个点,那么线段总条数为________.
![]() 3=2+1=
3=2+1=![]()
![]() 6=3+2+1=
6=3+2+1=![]()
![]()
(2)模型构建
如果线段上有m个点(包括线段的两个端点),那么共有________条线段.
(3)拓展应用
8位同学参加班上组织的象棋比赛,比赛采用单循环制(即每两位同学之间都要进行一场比赛),那么一共要进行多少场比赛?
请将这个问题转化为上述模型,并直接应用上述模型的结论解决问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,已知点A(﹣3,0)、B(0,4),对△OAB连续作旋转变换,依次得到△1、△2、△3、△4…,则△2016的直角坐标顶点的坐标为( )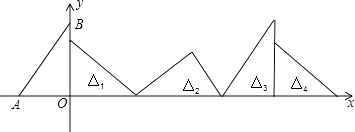
A.(8053,0)
B.(8064,0)
C.(8053, ![]() )
)
D.(8064, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了响应国家发展足球的战略方针,激发学生对足球的兴趣,特举办全员参与的“足球比赛”,赛后,全校随机抽查部分学生,其成绩(百分制)整理分成5组,并制成如下频数分布表和扇形统计图,请根据所提供的信息解答下列问题:
成绩频数分布表
组别 | 成绩(分) | 频数 |
A | 50≤x<60 | 6 |
B | 60≤x<70 | m |
C | 70≤x<80 | 20 |
D | 80≤x<90 | 36 |
E | 90≤x<100 | n |

(1)频数分布表中的m= , n=;
(2)样本中位数所在成绩的级别是 , 扇形统计图中,E组所对应的扇形圆心角的度数是;
(3)若该校共有2000名学生,请你估计体育综合测试成绩不少于80分的大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)直线y=kx+4经过点(1,2),求不等式kx+4≥0的解集.
(2)x取哪些正整数时,不等式 x+3>6 与 2x-1<10 都成立?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形ABCD中,动点F,E分别以相同的速度从D,C两点同时出发向C和B运动(任何一个点到达即停止),过点P作PM∥CD交BC于M点,PN∥BC交CD于N点,连接MN,在运动过程中, ①AE和BF的位置关系为;
②线段MN的最小值为 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com