
| A. | $\frac{b}{a}$>1 | B. | $\frac{a}{b}$<1 | C. | -a>-b | D. | a-b>0 |
分析 根据不等式的性质:不等式两边加(或减)同一个数(或式子),不等号的方向不变;不等式两边乘(或除以)同一个正数,不等号的方向不变;不等式两边乘(或除以)同一个负数,不等号的方向改变.可得答案.
解答 解:A、a<0时,不等号的方向改变,故A不符合题意;
B、b<0时,不等号的方向改变,故B不符合题意;
C、两边都乘以-1,不等号的方向改变,故C符合题意;
D、两边都减b,不等号的方向不变,故D不符合题意;
故选:C.
点评 主要考查了不等式的基本性质.“0”是很特殊的一个数,因此,解答不等式的问题时,应密切关注“0”存在与否,以防掉进“0”的陷阱.不等式的基本性质:不等式两边加(或减)同一个数(或式子),不等号的方向不变;不等式两边乘(或除以)同一个正数,不等号的方向不变;不等式两边乘(或除以)同一个负数,不等号的方向改变.


科目:初中数学 来源: 题型:填空题
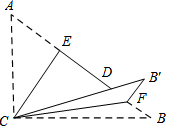 如图,Rt△ABC,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B'处,两条折痕与斜边AB分别交于点E、F,则线段CE的长等于$\frac{12}{5}$,线段B'F的长等于$\frac{4}{5}$.
如图,Rt△ABC,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B'处,两条折痕与斜边AB分别交于点E、F,则线段CE的长等于$\frac{12}{5}$,线段B'F的长等于$\frac{4}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4x-3(-9-3x)=3 | B. | 4x+3(-9-3x)=3 | C. | 4x-3(-9+3x)=3 | D. | 4x+3(-9+3x)=3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
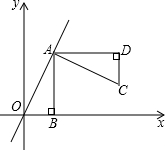 如图,正比例函数y=kx经过点A(2,4),AB⊥x轴于点B.
如图,正比例函数y=kx经过点A(2,4),AB⊥x轴于点B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com