
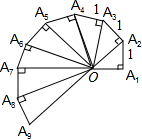
 ��ͼ�ǵ��߽������ѧ�������Ļ��ʾ��ͼ������ͼ������һ������ͼ��ʾ��ֱ���������ݻ����ɵģ����еĵ�һ��������OA1A2�ǵ���ֱ�������Σ���OA1=A1A2=A2A3��=A8A9=1��
��ͼ�ǵ��߽������ѧ�������Ļ��ʾ��ͼ������ͼ������һ������ͼ��ʾ��ֱ���������ݻ����ɵģ����еĵ�һ��������OA1A2�ǵ���ֱ�������Σ���OA1=A1A2=A2A3��=A8A9=1������ ��1�����ù��ɶ������μ��㼴�ɣ�
��2�����ݣ�1���ļ����ҳ����еĹ��ɿɵõ�OAn�ij���Ȼ�����ݼ����ǰ���������ε������Ȼ�����ݹ��ɽ����á�OAn-1An��������ɣ�
��3���������������г���ʽ��Ȼ������⼴�ɣ�
��� �⣺��1��OA2=$\sqrt{O{{A}_{1}}^{2}+{A}_{1}{{A}_{2}}^{2}}$=$\sqrt{2}$��OA3=$\sqrt{O{{A}_{2}}^{2}+{A}_{2}{{A}_{3}}^{2}}$=$\sqrt{3}$��OA4=$\sqrt{O{{A}_{3}}^{2}+{A}_{3}{{A}_{4}}^{2}}$=$\sqrt{4}$=2��
��
OA6=$\sqrt{6}$
�ʴ�Ϊ��$\sqrt{2}$��2��$\sqrt{6}$��
��2���ɣ�1����֪��OAn=$\sqrt{n}$��
S1=$\frac{1}{2}$��1��1=$\frac{1}{2}$��
S2=$\frac{1}{2}$��$\sqrt{2}$��$\frac{\sqrt{2}}{2}$��
S3=$\frac{1}{2}$��$\sqrt{3}$��1=$\frac{\sqrt{3}}{2}$��
��
��OAn-1An�����=$\frac{\sqrt{n-1}}{2}$��
��3��S12+S22+S32+��+S1002=��$\frac{1}{2}$��2+��$\frac{\sqrt{2}}{2}$��2+��$\frac{\sqrt{3}}{2}$��2+��+��$\frac{\sqrt{100}}{2}$��2=$\frac{1+2+3+��+100}{4}$=1262.5��
���� ������Ҫ������ǵ���ֱ�������ε������Լ����ɶ��������ú����ù��ɵ�̽�������⣬�ҳ����еĹ����ǽ���Ĺؼ���


 ����ѧ����ϵ�д�
����ѧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ƽ��ֱ������ϵ�У���B����Ϊ��1��-1������C����Ϊ��4��0������BCΪ����BC���Ϸ���һ��������ABCD����A��y���ϣ�����A��B��C��һ�������ߣ�
��ͼ����ƽ��ֱ������ϵ�У���B����Ϊ��1��-1������C����Ϊ��4��0������BCΪ����BC���Ϸ���һ��������ABCD����A��y���ϣ�����A��B��C��һ�������ߣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 7�� | B�� | 8�� | C�� | 9�� | D�� | 10�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 10�� | B�� | 11�� | C�� | 12�� | D�� | 13�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com