
分析 (1)观察三个化简过程,它们的共同特点是先变形分子,使分子出现含分母的因式,然后约分可化去分母中的根号;
(2)①利用二次根式的性质把a+3写成$\sqrt{x+3}$的平方形式,然后约分即可;、
②③都是利用平方差公式把分子分解,然后约分即可;
(3)利用分式的基本性质,把分子分母都乘以分母的有理化因式可化去分母中的根号.
解答 解:(1)上述各式化简过程的共同特点是:先将分子变形,通过约分.化去分母中的根号;
故答案为分子,分母;
(2)①$\frac{2a+6}{\sqrt{a+3}}$=$\frac{2(a+3)}{\sqrt{a+3}}$=$\frac{2(\sqrt{a+3})^{2}}{\sqrt{a+3}}$=2$\sqrt{a+3}$;
②$\frac{a-1}{1+\sqrt{a}}$=$\frac{(\sqrt{a})^{2}-1}{\sqrt{a}+1}$=$\frac{(\sqrt{a}+1)(\sqrt{a}-1)}{\sqrt{a}+1}$=$\sqrt{a}$-1;
③$\frac{a-b}{\sqrt{a}-\sqrt{b}}$=$\frac{(\sqrt{a})^{2}-(\sqrt{b})^{2}}{\sqrt{a}+\sqrt{b}}$=$\frac{(\sqrt{a}+\sqrt{b})(\sqrt{a}-\sqrt{b})}{\sqrt{a}+\sqrt{b}}$=$\sqrt{a}$-$\sqrt{b}$;
(3)把分子分母都乘以分母的有理化因式可化去上列各式分母中的根号.
点评 本题考查了分母有理化:分母有理化是指把分母中的根号化去;分母有理化常常是乘二次根式本身(分母只有一项)或与原分母组成平方差公式.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
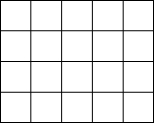 小猫在如图的地砖上随意走动,它停在任一块方砖上的机会均等,现在知道小猫停在红色方砖上的概率是$\frac{1}{4}$,试把红色方砖的颜色涂上阴影.
小猫在如图的地砖上随意走动,它停在任一块方砖上的机会均等,现在知道小猫停在红色方砖上的概率是$\frac{1}{4}$,试把红色方砖的颜色涂上阴影.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
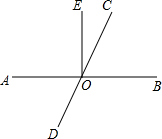 如图,已知AB,CD相交于点O,OE平分∠AOB,∠EOC=28°.
如图,已知AB,CD相交于点O,OE平分∠AOB,∠EOC=28°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com