
【题目】已知:A、B两点在直线l的同一侧,线段AO,BM均是直线l的垂线段,且BM在AO的右边,AO=2BM,将BM沿直线l向右平移,在平移过程中,始终保持∠ABP=90°不变,BP边与直线l相交于点P.
(1)当P与O重合时(如图2所示),设点C是AO的中点,连接BC.求证:四边形OCBM是正方形;
(2)请利用如图1所示的情形,求证:![]() =
=![]() ;
;
(3)若AO=2![]() ,且当MO=2PO时,请直接写出AB和PB的长.
,且当MO=2PO时,请直接写出AB和PB的长.
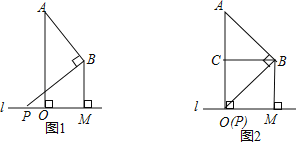
【答案】(1)证明见解析;(2)证明见解析;(3)当点P在O的右侧时, AB=3![]() ,BM=3;点P在O的左侧时,AB=
,BM=3;点P在O的左侧时,AB=![]() ,,PB=
,,PB=![]()
【解析】(1)先证明四边形OCBM是平行四边形,由于∠BMO=90°,所以OCBM是矩形,最后直角三角形斜边上的中线的性质即可证明四边形OCBM是正方形;
(2)连接AP、OB,由于∠ABP=∠AOP=90°,所以A、B、O、P四点共圆,从而利用圆周角定理可证明∠APB=∠OBM,所以△APB∽△OBM,利用相似三角形的性质即可求出答案.
(3)由于点P的位置不确定,故需要分情况进行讨论,共两种情况,第一种情况是点P在O的左侧时,第二种情况是点P在O的右侧时,然后利用四点共圆、相似三角形的判定与性质,勾股定理即可求出答案.
(1)∵2BM=AO,2CO=AO,
∴BM=CO,
∵AO∥BM,
∴四边形OCBM是平行四边形,
∵∠BMO=90°,
∴OCBM是矩形,
∵∠ABP=90°,C是AO的中点,
∴OC=BC,
∴矩形OCBM是正方形;
(2)连接AP、OB,
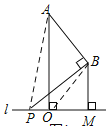
∵∠ABP=∠AOP=90°,
∴A、B、O、P四点共圆,
由圆周角定理可知:∠APB=∠AOB,
∵AO∥BM,
∴∠AOB=∠OBM,
∴∠APB=∠OBM,
∴△APB∽△OBM,
∴![]() ;
;
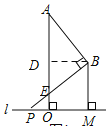
(3)当点P在O的左侧时,如图所示,
过点B作BD⊥AO于点D,
易证△PEO∽△BED,
∴![]() ,
,
易证:四边形DBMO是矩形,
∴BD=MO,OD=BM,
∴MO=2PO=BD,
∴![]() ,
,
∵AO=2BM=2![]() ,
,
∴BM=![]() ,
,
∴OE=![]() ,DE=
,DE=![]() ,
,
易证△ADB∽△ABE,
∴AB2=ADAE,
∵AD=DO=DM=![]() ,
,
∴AE=AD+DE=![]()
∴AB=![]() ,
,
由勾股定理可知:BE=![]() ,
,
易证:△PEO∽△PBM
∴![]() ,
,
∴PB=![]() ;
;
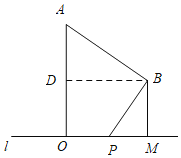
当点P在O的右侧时,如图所示,
过点B作BD⊥OA于点D,
∵MO=2PO,
∴点P是OM的中点,
设PM=x,BD=2x,
∵∠AOM=∠ABP=90°,
∴A、O、P、B四点共圆,
∴四边形AOPB是圆内接四边形,
∴∠BPM=∠A,
∴△ABD∽△PBM,
∴![]() ,
,
又易证四边形ODBM是矩形,AO=2BM,
∴AD=BM=![]() ,
,
∴![]() ,
,
解得:x=![]() ,
,
∴BD=2x=2![]()
由勾股定理可知:AB=3![]() ,BM=3.
,BM=3.


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:
【题目】张华发现某月的日历中一个有趣的问题,他用笔在上面画如图所示的十字框,若设任意一个十字框里的五个数为a、b、c、d、k.设中间的一个数为k,如图:试回答下列问题:
(1)此日历中能画出 个十字框?
(2)若a+b+c+d=84,求k的值;
(3)是否存在k的值,使得a+b+c+d=108,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AB=4,BC=2,将△ABC绕点B顺时针方向旋转到△A′BC′的位置,此时点A′恰好在CB的延长线上,则图中阴影部分的面积为_____(结果保留π).
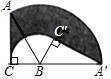
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提升教学效果,某学校决定购买甲、乙两种多媒体教学设备共100台投入新学期的使用.经学校研究决定,总购买金额不得超过535000元,已知每台甲、乙两种型号的多媒体仪器的单价分别为5000元和6000元.
(1)学校至少得购进多少台甲型多媒体仪器?
(2)在购买时,若学校要求甲型多媒体仪器的数量应少于乙型多媒体数量的2倍,则此次购买有几种方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图的方格地面上,标有编号A、B、C的3个小方格地面是空地,另外6个小方格地面是草坪,除此以外小方格地面完全相同.

(1)一只自由飞行的鸟,将随意地落在图中的方格地面上,问小鸟落在草坪上的概率是多少?
(2)现从3个小方格空地中任意选取2个种植草坪,则刚好选取A和B的2个小方格空地种植草坪的概率是多少(用树形图或列表法求解)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 ![]() ,已知
,已知![]() 中,AB=BC,
中,AB=BC,![]() ,点
,点 ![]() 为斜边
为斜边 ![]() 的中点,连接
的中点,连接 ![]() ,AF是
,AF是 ![]() 的平分线,分别与 BD、
的平分线,分别与 BD、![]() 相交于点 E、F.
相交于点 E、F.

(1)求证:![]() ;
;
(2)如图![]() ,连接
,连接 ![]() ,在不添加任何辅助线的条件下,直接写出图中所有的等腰三角形(不包含
,在不添加任何辅助线的条件下,直接写出图中所有的等腰三角形(不包含![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业工会开展“一周工作量完成情况”调查活动,随机调查了部分员工一周的工作量剩余情况,并将调查结果统计后绘制成如图1和图2所示的不完整统计图.
(1)被调查员工人数为 人:
(2)把条形统计图补充完整;
(3)若该企业有员工10000人,请估计该企业某周的工作量完成情况为“剩少量”的员工有多少人?
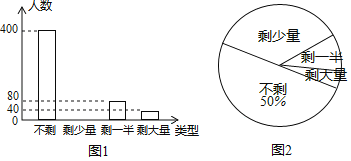
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=![]() ,∠B=
,∠B=![]() ,AC=1,BC=
,AC=1,BC=![]() ,AB=2,AC在直线l上,将△ABC绕点A顺时针转到位置①可得到点P1,此时AP1=2;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=2+
,AB=2,AC在直线l上,将△ABC绕点A顺时针转到位置①可得到点P1,此时AP1=2;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=2+![]() ;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=3+
;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=3+![]() …,按此顺序继续旋转,得到点P2016,则AP2016=( )
…,按此顺序继续旋转,得到点P2016,则AP2016=( )
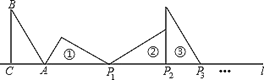
A. 2016+671![]() B. 2016+672
B. 2016+672![]()
C. 2017+671![]() D. 2017+672
D. 2017+672![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com