
【题目】如图,矩形ABCD中,AB=6,第1次平移将矩形ABCD沿AB的方向向右平移5个单位,得到矩形A1B1C1D1,第2次平移将矩形A1B1C1D1沿A1B1的方向向右平移5个单位,得到矩形A2B2C2D2…,第n次平移将矩形An﹣1Bn﹣1Cn﹣1Dn﹣1沿An﹣1Bn﹣1的方向平移5个单位,得到矩形AnBnCnDn(n>2).

(1)求AB1和AB2的长.
(2)若ABn的长为56,求n.
【答案】(1)AB1=11 AB2=16(2)n=10
【解析】
解:(1)∵AB=6,第1次平移将矩形ABCD沿AB的方向向右平移5个单位,得到矩形A1B1C1D1,
第2次平移将矩形A1B1C1D1沿A1B1的方向向右平移5个单位,得到矩形A2B2C2D2…,
∴AA1=5,A1A2=5,A2B1=A1B1﹣A1A2=6﹣5=1,
∴AB1=AA1+A1A2+A2B1=5+5+1=11.
∴AB2的长为:5+5+6=16.
(2)∵AB1=2×5+1=11,AB2=3×5+1=16,……,∴ABn=(n+1)×5+1.
∴由ABn=(n+1)×5+1=56解得:n=10.
(1)根据平移的性质得出AA1=5,A1A2=5,A2B1=A1B1﹣A1A2=6﹣5=1,进而求出AB1和AB2的长.
(2)根据(1)中所求得出数字变化规律,进而得出ABn=(n+1)×5+1求出n即可.


科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AC=BC,点D、E、F分别是线段AC、BC、AD的中点,BF、ED的延长线交于点G,连接GC.
(1)求证:AB=GD;
(2)当CG=EG时,且AB=2,求CE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F,连接BD.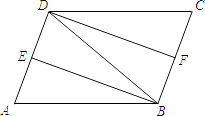
(1)求证:△ABE≌△CDF;
(2)若AB=DB,求证:四边形DFBE是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
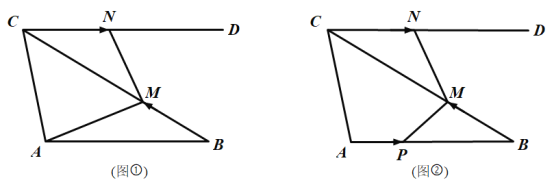
【题目】如图①,在![]() 中,
中,![]() cm ,
cm ,![]() cm,过点
cm,过点![]() 作射线
作射线![]() .点
.点![]() 从点
从点![]() 出发,以3 cm/s的速度沿
出发,以3 cm/s的速度沿![]() 匀速移动;点
匀速移动;点![]() 从点
从点![]() 出发,以
出发,以![]() cm/s的速度沿
cm/s的速度沿![]() 匀速移动.点
匀速移动.点![]() 、
、![]() 同时出发,当点
同时出发,当点![]() 到达点
到达点![]() 时,点
时,点![]() 、
、![]() 同时停止移动.连接
同时停止移动.连接![]() 、
、![]() ,设移动时间为
,设移动时间为![]() (s).
(s).
(1)点![]() 、
、![]() 从移动开始到停止,所用时间为 s;
从移动开始到停止,所用时间为 s;
(2)当![]() 与
与![]() 全等时,
全等时,
①若点![]() 、
、![]() 的移动速度相同,求
的移动速度相同,求![]() 的值;
的值;
②若点![]() 、
、![]() 的移动速度不同,求
的移动速度不同,求![]() 的值;
的值;
(3)如图②,当点![]() 、
、![]() 开始移动时,点
开始移动时,点![]() 同时从点
同时从点![]() 出发,以2 cm/s的速度沿
出发,以2 cm/s的速度沿![]() 向点
向点![]() 匀速移动,到达点
匀速移动,到达点![]() 后立刻以原速度沿
后立刻以原速度沿![]() 返回.当点
返回.当点![]() 到达点
到达点![]() 时,点
时,点![]() 、
、![]() 、
、![]() 同时停止移动.在移动的过程中,是否存在
同时停止移动.在移动的过程中,是否存在![]() 与
与![]() 全等的情形?若存在,求出
全等的情形?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乘法公式的探究及应用.

小题1:如图1,可以求出阴影部分的面积是_______ (写成两数平方差的形式);
小题2:如图2,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是_______,长是______,面积是_________ (写成多项式乘法的形式).
小题3:比较图 1,图2的阴影部分面积,可以得到乘法公式________ (用式子表达).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,击打台球时小球反弹前后的运动路线遵循对称原理,即小球反弹前后的运动路线与台球案边缘的夹角相等(α=β),在一次击打台球时,把位于点P处的小球沿所示方向击出,小球经过5次反弹后正好回到点P,若台球案的边AD的长度为4,则小球从P点被击出到回到点P,运动的总路程为( )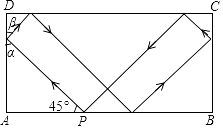
A.16
B.16 ![]()
C.20
D.20 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
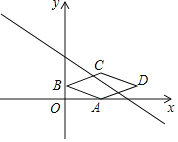
【题目】如图,在平面直角坐标系xOy中,菱形ABCD的顶点A的坐标为(2,0),点B的坐标为(0,1),对角线BD与x轴平行,若直线y=kx+5+2k(k≠0)与菱形ABCD有交点,则k的取值范围是( )
A.![]() B.
B.![]()
C.![]() D.﹣2≤k≤2且k≠0
D.﹣2≤k≤2且k≠0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com