
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案科目:初中数学 来源: 题型:
 在一次探究性活动中,教师提出了问题:已知矩形的长和宽分别是2和1,是否存在另一个矩形,它的周长和面积分别是已知矩形周长和面积的2倍?设所求矩形的长和宽分别为x,y
在一次探究性活动中,教师提出了问题:已知矩形的长和宽分别是2和1,是否存在另一个矩形,它的周长和面积分别是已知矩形周长和面积的2倍?设所求矩形的长和宽分别为x,y| 4 |
| x |
| 4 |
| x |
|
|
查看答案和解析>>
科目:初中数学 来源: 题型:
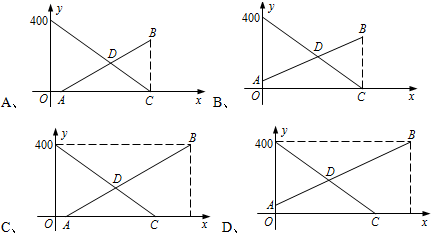
 (2013•建邺区一模)甲、乙两观光船分别从A、B两港同时出发,相向而行,两船在静水中速度相同,水流速度为5千米/小时,甲船逆流而行4小时到达B港.下图表示甲观光船距A港的距离y(千米)与行驶时间x(小时)之间的函数关系式,结合图象解答下列问题:
(2013•建邺区一模)甲、乙两观光船分别从A、B两港同时出发,相向而行,两船在静水中速度相同,水流速度为5千米/小时,甲船逆流而行4小时到达B港.下图表示甲观光船距A港的距离y(千米)与行驶时间x(小时)之间的函数关系式,结合图象解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•南京二模)甲车以某一速度沿公路从A地匀速驶往B地,到达B地停留m小时后,立即以原速沿原路匀速返回A地,共用11小时.甲车出发一段时间后,乙车沿同一条公路以每小时120千米的速度从A地匀速驶往B地,甲车从A地出发9小时后,两车在距离A地160千米处相遇,甲车回到A地的同时乙车到达了B地.如图所示的折线是甲车离A地的距离y1(千米)与行驶时间 x(小时)之间的函数图象.
(2013•南京二模)甲车以某一速度沿公路从A地匀速驶往B地,到达B地停留m小时后,立即以原速沿原路匀速返回A地,共用11小时.甲车出发一段时间后,乙车沿同一条公路以每小时120千米的速度从A地匀速驶往B地,甲车从A地出发9小时后,两车在距离A地160千米处相遇,甲车回到A地的同时乙车到达了B地.如图所示的折线是甲车离A地的距离y1(千米)与行驶时间 x(小时)之间的函数图象.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com