
【题目】已知∠BOC=60°,OF平分∠BOC.若AO⊥BO,OE平分∠AOC,则∠EOF的度数是( )
A. 45°
B. 15°
C. 30°或60°
D. 45°或15°
【答案】A
【解析】
根据垂线的定义,可得∠AOB的度数,根据角的和差,可得∠AOC的度数,根据角平分线的性质,可得∠COE、∠COF的度数,根据角的和差,可得答案.
如图1,

由AO⊥BO,得∠AOB=90°,
由角的和差,得∠AOC=∠AOB+∠BOC=150°,
∵OE平分∠AOC,OF平分∠BOC,
∴∠COE=![]() ∠AOC=
∠AOC=![]() ×150°=75°,∠COF=
×150°=75°,∠COF=![]() ∠BOC=
∠BOC=![]() ×60°=30°,
×60°=30°,
由角的和差,得∠EOF=∠COE-∠COF=75°-30°=45°;
如图2,

由AO⊥BO,得∠AOB=90°,
由角的和差,得∠AOC=∠AOB-∠BOC=30°,
∵OE平分∠AOC,OF平分∠BOC,
∴∠COE=![]() ∠AOC=
∠AOC=![]() ×30°=15°,∠COF=
×30°=15°,∠COF=![]() ∠BOC=
∠BOC=![]() ×60°=30°,
×60°=30°,
由角的和差,得∠EOF=∠COE+∠COF=15°+30°=45°,
故选A.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
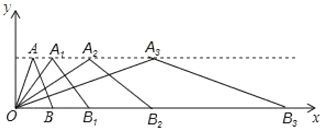
【题目】如图,在平面直角坐标系中,第一次将三角形![]() 变换成三角形
变换成三角形![]() ,第二次将三角形
,第二次将三角形![]() 变换成三角形
变换成三角形![]() ,第三次将三角形变换成三角形
,第三次将三角形变换成三角形![]() ,已知
,已知![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)观察每次变换前后的三角形,找出规律,按这些变换规律将三角形![]() 变换成三角形
变换成三角形![]() ,求
,求![]() 和
和![]() 的坐标;
的坐标;
(2)若按第(1)题的规律将三角形![]() 进行了
进行了![]() 次变换,得到三角形
次变换,得到三角形![]() ,请推测
,请推测![]() 和
和![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是△ABC的内心,AE的延长线交BC于点F,交△ABC的外接圆⊙O于点D,连接BD,过点D作直线DM,使∠BDM=∠DAC. (Ⅰ)求证:直线DM是⊙O的切线;
(Ⅱ)求证:DE2=DFDA.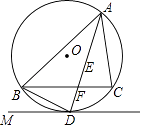
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3cm,BC=6cm.点P从点D出发向点A运动,运动到点A即停止;同时,点Q从点B出发向点C运动,运动到点C即停止,点P、Q的速度都是1cm/s.连接PQ、AQ、CP.设点P、Q运动的时间为ts.
当t为何值时,四边形ABQP是矩形;
当t为何值时,四边形AQCP是菱形;
分别求出(2)中菱形AQCP的周长和面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点F、C是⊙O上两点,且 ![]() =
= ![]() =
= ![]() ,连接AC、AF,过点C作CD⊥AF,交AF的延长线于点D,垂足为D,若CD=2
,连接AC、AF,过点C作CD⊥AF,交AF的延长线于点D,垂足为D,若CD=2 ![]() ,则⊙O的半径为( )
,则⊙O的半径为( ) 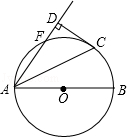
A.2 ![]()
B.4 ![]()
C.2
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直线AB交CD于点O,OE平分∠BOD,OF平分∠COB,∠AOD∶∠BOE=4∶1,则∠AOF等于( )

A. 130°
B. 120°
C. 110°
D. 100°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:∠MON=80°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O 重合),连接AC交射线OE于点D.设∠OAC=x°.
(1)如图1,若AB∥ON,则:①∠ABO的度数是 ;
②如图2,当∠BAD=∠ABD时,试求x的值(要说明理由);
(2)如图3,若AB⊥OM,则是否存在这样的X的值,使得△ADB中有两个相等的角?若存在,直接写出x的值;若不存在,说明理由.(自己画图)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为坐标原点,过点A(8,6)分别做x轴、y轴的平行线,交y轴于点B,交x轴于点C,点P是从点B出发,沿B→A→C以2个单位长度/秒的速度向终点C运动的一个动点,运动时间为t(秒).
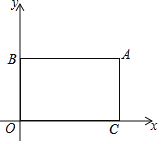
(1)直接写出点B和点C的坐标:B( , )C( , ).
(2)当点P运动时,用含t的代数式表示线段AP的长,并写出t的取范围;
(3)点D(2,0),连结PD、AD,在(2)的条件下是否存在这样的t值,使S△APD=![]() S四边形ABOC,若存在,请求t值,若不存在,请说明理由.
S四边形ABOC,若存在,请求t值,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com