
【题目】一天课间,顽皮的小明同学拿着老师的等腰直角三角板(AC=BC,∠ACB=90°)玩,不小心掉到两根直立于地面的柱子(∠ADC=∠BEC=90°)之间,如图所示,这一幕恰巧被数学老师看见了,于是有了下面这道题.
(1)求证:△ADC≌△CEB;
(2)如果每块砖的厚度a=10cm,请你帮小明求出三角板ABC的面积.

【答案】(1)见解析;(2)1250cm2
【解析】
(1)根据同角的余角相等可得∠DAC=∠BCE,然后利用AAS即可证明△ADC≌△CEB;
(2)根据题意可得AD=40cm,BE=30cm,根据全等三角形的性质和勾股定理可求出BC=50cm,然后根据三角形面积公式求解.
解:(1)∵∠ACB=90°,∠ADC=∠BEC=90°,
∴∠DAC+∠ACD=90°,∠ACD+∠BCE=90°,
∴∠DAC=∠BCE,
又∵AC=BC,
∴△ADC≌△CEB(AAS);
(2)∵每块砖的厚度a=10cm,
∴AD=40cm,BE=30cm,
∵△ADC≌△CEB,
∴AD=CE=40cm,
∴BC=![]() cm,
cm,
∴AC=BC=50cm,
∴三角板ABC的面积=![]() cm2.
cm2.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:
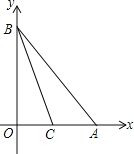
【题目】如图,点A和点B分别在x轴和y轴上,且OA=OB=4,直线BC交x轴于点C,S△BOC=S△ABC.
(1)求直线BC的解析式;
(2)在直线BC上求作一点P,使四边形OBAP为平行四边形(尺规作图,保留痕迹,不写作法).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个长方形运动场被分隔成A,B,A,B,C共5个区,A区是边长为a m的正方形,C区是边长为c m的正方形.
(1)列式表示每个B区长方形场地的周长,并将式子化简;
(2)列式表示整个长方形运动场的周长,并将式子化简;
(3)如果a=40,c=10,求整个长方形运动场的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暴雨过后,某地遭遇山体滑坡,武警总队派出一队武警战士前往抢险. 半小时后,第二队前去支援,平均速度是第一队的1.5倍,结果两队同时到达.已知抢险队的出发地与灾区的距离为90千米,两队所行路线相同,问两队的平均速度分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着通讯市场竞争的日益激烈,为了占领市场,甲公司推出的优惠措施是:每分钟降低![]() 元后,再下调
元后,再下调![]() ;乙公司推出的优惠措施是:每分钟下调
;乙公司推出的优惠措施是:每分钟下调![]() 后,再降低
后,再降低![]() 元.已知甲、乙两公司原来每分钟收费标准相同,都是
元.已知甲、乙两公司原来每分钟收费标准相同,都是![]() 元.
元.
(1)用含![]() ,
,![]() 的式子表示甲、乙两公司推出优惠措施后每分钟的收费标准;
的式子表示甲、乙两公司推出优惠措施后每分钟的收费标准;
(2)推出优惠措施后哪家公司的收费便宜?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
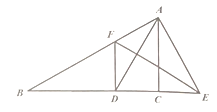
【题目】如图所示,在![]() 中,
中,![]() 是
是![]() 平分线,
平分线,![]() 的垂直平分线分别交
的垂直平分线分别交![]() 延长线于点
延长线于点![]() .求证:
.求证:![]() .
.
证明:∵![]() 平分
平分![]()
∴![]()
![]() (角平分线的定义)
(角平分线的定义)
∵![]() 垂直平分
垂直平分![]()
∴ ![]() (线段垂直平分线上的点到线段两个端点距离相等)
(线段垂直平分线上的点到线段两个端点距离相等)
∴![]() ( )
( )
∴![]() (等量代换)
(等量代换)
∴![]() ( )
( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长为60cm,宽为x(cm)的大长方形被分割为7小块,除阴影 A, B外,其余5块是形状、大小完全相同的小长方形,其较短一边长为 y (cm).

(1)填空:从图可知,每个小长方形较长的一边长是_________cm (用含y的代数式表示).
(2)分别求出阴影 A,B的面积,并计算阴影 A,B的面积差?(用含x,y的式子表示)
(3)当y=10时,阴影 A与阴影 B的面积差会随着x的变化而变化吗?请你作出判断,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com