
【题目】已知∠AOB是一个直角,作射线OC,再分别作∠AOC和∠BOC的平分线OD、OE.
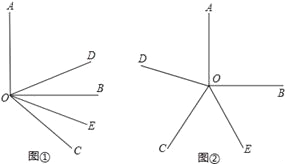
(1)如图①,当∠BOC=70°时,求∠DOE的度数;
(2)如图②,当射线OC在∠AOB内绕O点旋转时,∠DOE的大小是否发生变化若变化,说明理由;若不变,求∠DOE的度数;
(3)如图③,当射线OC在∠AOB外绕O点旋转时,画出图形,判断∠DOE的大小是否发生变化若变化,说明理由;若不变,求∠DOE的度数.

【答案】(1)∠DOE=45°;(2)∠DOE的大小不变等于45°.理由见解析;(3)∠DOE的大小发生变化,∠DOE=45°或135.
【解析】试题分析:(1)根据角平分线的定义,OD、OE分别平分∠AOC和∠BOC,则可求得∠COE、∠COD的值,∠DOE=∠COE+∠COD;
(2)结合角的特点,∠DOE=∠DOC+∠COE,求得结果进行判断和计算;
(3)正确作出图形,判断大小变化.
试题解析:
解:(1)∵OD、OE分别平分∠AOC和∠BOC,
∴∠COE=![]() ∠COB=35°,∠COD=
∠COB=35°,∠COD=![]() ∠AOC=10°,
∠AOC=10°,
∴∠DOE=45°;
(2)∠DOE的大小不变等于45°.
理由:∠DOE=∠DOC+∠COE=![]() ∠COB+
∠COB+![]() ∠AOC
∠AOC
=![]() (∠COB+∠AOC)
(∠COB+∠AOC)
=![]() ∠AOB=45°;
∠AOB=45°;
(3)∠DOE的大小发生变化,∠DOE=45°或135.
如图①,∠DOE=45°;
如图②,∠DOE=135°.(说理过程同(2))
点睛: 此题主要考查了角平分线的性质以及角的有关计算,正确作图,熟记角的特点与角平分线的定义是解决此题的关键.


科目:初中数学 来源: 题型:
【题目】(1)已知在△ABC中,∠A=90°,∠B=67.5°,请画一条直线,把这个三角形分割成两个等腰三角形(请你选用下面给出的备用图,把所有不同的分割方法都画出来.只需画图,不必说明理由,但要在图中标出相等两角的度数).
(2)已知在△ABC中,∠C是其最小的内角,过顶点B的一条直线把这个三角形分割成了两个等腰三角形,请探求∠ABC与∠C之间的关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点F是BC延长线上一点,以CF为边,作菱形CDEF,使菱形CDEF与点A在BC的同侧,连接BE,点G是BE的中点,连接AG、DG.
(1)如图①,当∠BAC=∠DCF=90°时,直接写出AG与DG的位置和数量关系;
(2)如图②,当∠BAC=∠DCF=60°时,试探究AG与DG的位置和数量关系,
(3)当∠BAC=∠DCF=α时,直接写出AG与DG的数量关系.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com