
分析 如图,⊙I是△ABC的内切圆,作ID⊥AB于D,IE⊥BC于E,IF⊥AC于F,连接IA、IB、IC,根据S△ABC=S△AIB+S△CIB+S△AIC进行计算即可得到结论.
解答 证明:如图,⊙I是△ABC的内切圆,作ID⊥AB于D,IE⊥BC于E,IF⊥AC于F,连接IA、IB、IC,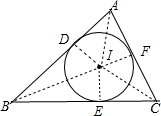
∵⊙I为△ABC的内切圆,
∴ID=IE=IF=r,
∵S△AIB=$\frac{1}{2}$AB•ID,S△CIB=$\frac{1}{2}$BC•IE,S△AIC=$\frac{1}{2}$AC•IF,
∴S△ABC=S△AIB+S△CIB+S△AIC=$\frac{1}{2}$cr+$\frac{1}{2}$ar+$\frac{1}{2}$br=$\frac{1}{2}$r(a+b+c)=pr.
点评 本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.三角形的内心就是三角形三个内角角平分线的交点,解题的关键是学会利用分割法求三角形面积,属于中考常考题型.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某校期中考试后,为了更好地了解七年级测试的数学成绩情况,随机抽取了部分学生的试卷.对学生的数学成绩(得分取整数)进行赘理.分成五组,并绘制成如下不完整的频数分布直方图.在直方图中从左到右依次为一、二、三、四、五组.成绩没有低于20分的,第五组的人数占抽样人数的30%.第四组的人数是第二组的人数的4倍.请结合信息回答下列问题.
某校期中考试后,为了更好地了解七年级测试的数学成绩情况,随机抽取了部分学生的试卷.对学生的数学成绩(得分取整数)进行赘理.分成五组,并绘制成如下不完整的频数分布直方图.在直方图中从左到右依次为一、二、三、四、五组.成绩没有低于20分的,第五组的人数占抽样人数的30%.第四组的人数是第二组的人数的4倍.请结合信息回答下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
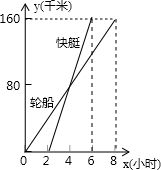 如图,表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行驶过程中随时间变化的图象(分别是正比例函数和一次函数图象),根据图象解答下列问题;
如图,表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行驶过程中随时间变化的图象(分别是正比例函数和一次函数图象),根据图象解答下列问题;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com