
【题目】如图,在△ABC中,∠C = 90°,以AC为直径的⊙O交AB于点D,连接OD,点E在BC上, B E=DE.

(1)求证:DE是⊙O的切线;
(2)若BC=6,求线段DE的长;
(3)若∠B=30°,AB =8,求阴影部分的面积(结果保留![]() ).
).
【答案】(1)详见解析;(2)3;(3)![]()
【解析】
(1)根据OA=OD,BE=DE,得∠A=∠1,∠B=∠2,根据∠ACB=90°,即可得∠1+∠2=90°,即可得OD⊥DE,从而可证明结论;
(2)连接CD,根据现有条件推出CE是⊙O的切线,再结合DE是⊙O的切线,推出DE=CE又BE=DE,即可得出DE;
(3)过O作OG⊥AD,垂足为G,根据已知条件推出AD,AG和OG的值,再根据![]() ,即可得出答案.
,即可得出答案.
解:(1)证明:∵OA=OD,BE=DE,
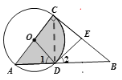
∴∠A=∠1,∠B=∠2,
∵△ABC中,∠ACB=90°,
∴∠A+∠B=90°,
∴∠1+∠2=90°,
∴∠ODE=180°-(∠1+∠2)=90°,
∴OD⊥DE,又OD为⊙O的半径,
∴DE是⊙O的切线;
(2)连接CD,则∠ADC=90°,
∵∠ACB=90°,
∴AC⊥BC,又AC为⊙O的直径,
∴CE是⊙O的切线,又DE是⊙O的切线,
∴DE=CE又BE=DE,
∴DE=CE=BE=![]() ;
;
(3)过O作OG⊥AD,垂足为G,则![]() ,
,
∵Rt△ABC中,∠B=30°,AB=8,
∴AC=![]() ,∠A=60°(又OA=OD),
,∠A=60°(又OA=OD),
∴∠COD=120°,△AOD为等边三角形,
∴AD=AO=OD=![]() 2,
2,
∴![]() ,
,
∴OG![]() ,
,
∴![]() ,
,
∴阴影部分的面积为![]() .
.


科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+3x+c(a,c为常数,且a≠0)经过点(﹣1,﹣1),(0,3),有下列结论:
①ac<0;
②当x>1时,y的值随x值的增大而减小;
③3是方程ax2+2x+c=0的一个根;
④当﹣1<x<3时,ax2+2x+c>0
其中正确结论的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在三角形ABC中,AB=10,AC=BC=13,以BC为直径作⊙O交AB于点D,交AC于点G,直线DF⊥AC,于点F,交CB的延长线于点E.
(1)求证:DF是⊙O的切线;
(2)求cos∠ADF的值.
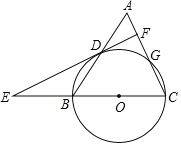
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果抛物线m的顶点在抛物线n上,同时抛物线n的顶点在抛物线m上,那么我们就称抛物线m与n为交融抛物线.
(1)已知抛物线a:![]() ,判断下列抛物线b:
,判断下列抛物线b:![]() ,c:
,c:![]() 与已知抛物线a是否为交融抛物线?并说明理由;
与已知抛物线a是否为交融抛物线?并说明理由;
(2)在直线y=2上有一动点P(t,2),将抛物线a:![]() 绕点P(t,2)旋转180得到抛物线l,若抛物线a与l为交融抛物线,求抛物线l的解析式;
绕点P(t,2)旋转180得到抛物线l,若抛物线a与l为交融抛物线,求抛物线l的解析式;
(3)M为抛物线a:![]() 的顶点,Q为抛物线a的交融抛物线的顶点,是否存在以MQ为斜边的等腰直角三角形MQS,使直角顶点S在y轴上?若存在,求出点S的坐标;若不存在,请说明理由.
的顶点,Q为抛物线a的交融抛物线的顶点,是否存在以MQ为斜边的等腰直角三角形MQS,使直角顶点S在y轴上?若存在,求出点S的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() =
=![]() 与
与![]() 轴交于点
轴交于点![]() ,其对称轴为直线
,其对称轴为直线![]() ,结合图象分析下列结论:
,结合图象分析下列结论:
① ![]() ; ②
; ② ![]() ;
;
③ ![]() >0; ④当
>0; ④当![]() 时,
时,![]() 随
随![]() 的增大而增大;
的增大而增大;
⑤ ![]() ≤
≤![]() (m为实数),其中正确的结论有( )
(m为实数),其中正确的结论有( )
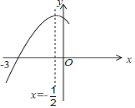
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场举办抽奖活动,规则如下:在不透明的袋子中有2个红球和2个黑球,这些球除颜色外都相同,顾客每次摸出一个球,若摸到红球,则获得1份奖品,若摸到黑球,则没有奖品。
(1)如果小芳只有一次摸球机会,那么小芳获得奖品的概率为 ;
(2)如果小芳有两次摸球机会(摸出后不放回),求小芳获得2份奖品的概率。(请用“画树状图”或“列表”等方法写出分析过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y= 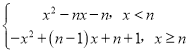 (n为常数)
(n为常数)
(1)若点(3,-7)在函数图象上,求n的值;
(2)当y=1时,求自变量x的值(用含n的代数式表示);
(3)若n-2≤x≤n+1,设函数的最小值为y0.当-5≤y0≤-2时,求n的取值范围;
(4)直接写出函数图象与直线y=-x+4有两个交点时,n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
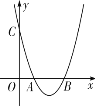
【题目】如图,已知二次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,与y轴交于点
,与y轴交于点![]() .
.
(1)求二次函数的解析式;
(2)若点P为抛物线上的一点,点F为对称轴上的一点,且以点ABPF为顶点的四边形为平行四边形,求点P的坐标;
(3)点E是二次函数第四象限图象上一点,过点E作x轴的垂线,交直线BC于点D,求四边形![]() 面积的最大值及此时点E的坐标.
面积的最大值及此时点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一张正方形ABCD纸片,边长AB=2,按步骤进行折叠,如图1,先将正方形纸片ABCD对折,得到折痕EF;再折出矩形BCFE的对角线BF.
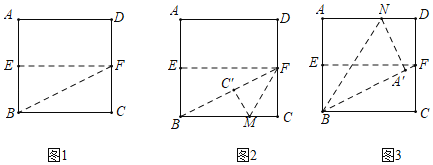
(1)如图2,将CF边折到BF上,得到折痕FM,点C的对应点为C',求CM的长.
(2)如图3,将AB边折到BF上,得到折痕BN,点A的对应点为A',求AN的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com