
【题目】已知:如图,在矩形ABCD中,![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 的中点,
的中点,![]() ,
,![]() 分别是线段
分别是线段![]() ,
,![]() 的中点.
的中点.
(1)求证:![]() ≌
≌![]() ;
;
(2)判断四边形![]() 是什么特殊四边形,并证明你的结论;
是什么特殊四边形,并证明你的结论;
(3)当四边形![]() 是正方形时,求
是正方形时,求![]() 的值.
的值.

【答案】(1)证明见解析(2)四边形MENF是菱形(3)2
【解析】分析:(1)因为M为AD中点,根据全等三角形的判定定理推出即可;
(2)根据三角形中位线定理求出NE∥MC,NF=MB,得出平行四边形,求出BM=CM,推出ME=MF,根据菱形的判定推出即可;
(3)求出∠EMF=90°,根据正方形的判定推出即可.
详解:(1)证明:∵四边形![]() 是矩形,
是矩形,
∴![]() ,
,![]()
![]() 90°,
90°,
又∵![]() 是
是![]() 的中点, ∴
的中点, ∴![]() .
.
在![]() 和
和![]() 中,
中,
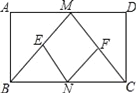
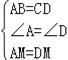 ,
,
∴![]() ≌
≌![]() .
.
(2)解:四边形![]() 是菱形.
是菱形.
∵![]() 分别是
分别是![]() 的中点,
的中点,
∴![]() ∥
∥![]() ,
,![]() .
.
∴四边形![]() 是平行四边形.
是平行四边形.
由(1),得![]() ∴
∴![]() .
.
∴四边形![]() 是菱形.
是菱形.
(3)解:∵四边形![]() 是正方形.
是正方形.
∴![]() ,
,
又∵![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
∴![]()
又∵![]() 是
是![]() 的中点,
的中点,
∴![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知数轴上三点M,O,N对应的数分别为-1,0,3,点P为数轴上任意一点,其对应的数为x.
![]()
(1)MN的长为 ;
(2)如果点P到点M、点N的距离相等,那么x的值是 ;
(3)数轴上是否存在点P,使点P到点M、点N的距离之和是8?若存在,直接写出x的值;若不存在,请说明理由.
(4)如果点P以每分钟1个单位长度的速度从点O向左运动,同时点M和点N分别以每分钟2个单位长度和每分钟3个单位长度的速度也向左运动.设t分钟时点P到点M、点N的距离相等,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为支持抗震救灾,我市A、B两地分别有赈灾物资100吨和180吨,需全部运往重灾区C、D两县,根据灾区的情况,这批赈灾物资运往C县的数量比运往D县的数量的2倍少80吨.
(1)求这批赈灾物资运往C、D两县的数量各是多少吨?
(2)设A地运往C县的赈灾物资数量为x吨(x为整数).若要B地运往C县的赈灾物资数量大于A地运往D县赈灾物资数量的2倍,且要求B地运往D县的赈灾物资数量不超过63吨,则A、B两地的赈灾物资运往C、D两县的方案有几种?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一名足球守门员练习折返跑,从球门线出发,向前记作正数,返回记作负数,他的记录如下:(单位:米)+5,-3,+10,-8,-6,+12,-10
(1)守门员最后是否回到了球门线的位置?
(2)在练习过程中,守门员离开球门最远距离是多少米?
(3)守门员全部练习结束后,他共跑了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在△ABC中,AB=AC.过A点的直线a从与边AC重合的位置开始绕点A按顺时针方向旋转角θ,直线a交BC边于点P(点P不与点B、点C重合),△BMN的边MN始终在直线a上(点M在点N的上方),且BM=BN,连接CN.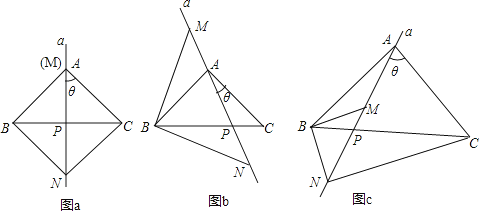
(1)当∠BAC=∠MBN=90°时,
①如图a,当θ=45°时,∠ANC的度数为△;
②如图b,当θ≠45°时,①中的结论是否发生变化?说明理由;
(2)如图c,当∠BAC=∠MBN≠90°时,请直接写出∠ANC与∠BAC之间的数量关系,不必证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠A=60°,AC=a,作斜边AB边中线CD,得到第一个三角形ACD;DE⊥BC于点E,作Rt△BDE斜边DB上中线EF,得到第二个三角形DEF;依此作下去…则第n个三角形的面积等于 . 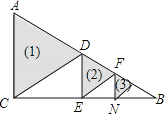
查看答案和解析>>
科目:初中数学 来源: 题型:
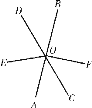
【题目】如图,已知直线AB,CD相交于点O,OE平分∠AOD,FO⊥AB,垂足为O,![]() ∠BOD=∠DOE.
∠BOD=∠DOE.
(1)求∠BOF的度数;
(2)请写出图中与∠BOD相等的所有的角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴是一个非常重要的数学工具,它使数和数轴上的点建立对应关系,解释了数与点之间的内在联系,它是“数形结合”的基础。
如图,数轴上有三个点A、B、C,它们可以沿着数轴左右移动,请回答
![]() )
)
(1)将点B向右移动4个单位长度后到达点D,点D表示的数是 ,A、D两点之间的距离是 ;
(2)移动点A到达E点,使B、C、E三点的其中某一点到其它两点的距离相等,写出点E在数轴上对应的数值 ;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com