
����Ŀ����������������������ߣ��۹������Ѿ���Ϊ�������жȼٵ�һ�ַ�ʽ�����ڼ��ڵİ��ţ����β�������绰��̸�������������˽����Ǽ��ڼ�ѡ�������������ͣ������Ρ����ڳ����Ρ������κ����������ݵ绰��̸�Ľ���Ƴ�ͳ��ͼ������û��������ɵ�ͳ��ͼ�ṩ����Ϣ�ش��������⣮
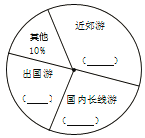
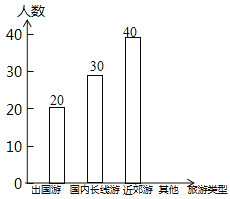
��1��ѡ��������ʽ�������Ƕ��٣�
��2����ȫ����ͳ��ͼ������ͳ��ͼ��
��3����A��B�� 4��3���ڢ١�����ѩɽ�����ڰ��ʹ���͢��³����������ط���ѡ�����е�һ�ط����森���������㱻A��Bѡ�еĿ�������ͬ��������״ͼ�����б���д��A��B����ѡ������п��ܽ��������A��B����ѡ���ڲ�ͬ�ط�����ĸ��ʣ�����״ͼ�����б�����ֱ����ÿ������ǰ�����ַ��ż��ɣ�
���𰸡���1��ѡ��������ʽ����10������2��������(3) ![]()
����������������1��������ͳ��ͼ�õ������Ρ����ڳ����Ρ������ε�����������������ͼ�ó����Ӧ�İٷֱȣ��ɼ������������Ȼ�������������10%���ɣ�
��2���ȼ���������Ρ����ڳ����Ρ���������ռ�İٷֱȣ�Ȼ��ȫͳ��ͼ��
��3���Ȼ���״ͼչʾ����9�ֵȿ��ܵĽ���������ҳ�A��B����ѡ���ڲ�ͬ�ط�����Ľ������Ȼ����ݸ��ʹ�ʽ��⣮
��⣺��1����20+30+40���£�1��10%��=100��100��10%=10��
��ѡ��������ʽ����10��
��2����������ռ�İٷֱ�Ϊ40%�����ڳ�������ռ�İٷֱ�Ϊ30%����������ռ�İٷֱ�Ϊ20%��
��ͼ��

��3������״ͼΪ��

����9�ֵȿ��ܵĽ������A��B����ѡ���ڲ�ͬ�ط�����Ľ����Ϊ6��
����A��B����ѡ���ڲ�ͬ�ط�����ĸ���=![]() =
=![]() ��
��


 ��ѧ����ͬ����ϰϵ�д�
��ѧ����ͬ����ϰϵ�д� ��ǰ�κ�ͬ����ϰϵ�д�
��ǰ�κ�ͬ����ϰϵ�д� ����С��ҵϵ�д�
����С��ҵϵ�д� �Ƹ�С״Ԫ����������ϰ��ϵ�д�
�Ƹ�С״Ԫ����������ϰ��ϵ�д� �ɹ�ѵ���ƻ�ϵ�д�
�ɹ�ѵ���ƻ�ϵ�д� ����ѵ����ֱͨ�п�����ϵ�д�
����ѵ����ֱͨ�п�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ֵ���Ʊÿ��10Ԫ��һ����ʹ�ã����ǵ����ǵIJ�ͬ����ҲΪ������������οͣ����ֳ�����ԭ������Ʊ�����⣬���Ƴ���һ�֡����������Ʊ������Ʊ������������Ʊ�ӹ������𣬿ɹ���Ʊ��ʹ��һ�꣩����Ʊ��A��B��C���࣬A����Ʊÿ��120Ԫ����Ʊ�߽�����ʱ�������ٹ�����Ʊ��B����Ʊÿ��60Ԫ����Ʊ�߽������ʱ�����ٹ�����Ʊ��ÿ��2Ԫ��C����Ʊÿ��40Ԫ����Ʊ�߽������ʱ�����ٹ�����Ʊ��ÿ��3Ԫ��
��1�������ֻѡ��һ�ֹ�����Ʊ�ķ�ʽ��������ƻ���һ������80Ԫ���ڸ��ֵ���Ʊ�ϣ���ͨ�����㣬�ҳ���ʹ������ֵĴ������Ĺ�Ʊ��ʽ����༸�Σ�
��2����һ���н�����ֳ������ٴ�ʱ������A����Ʊ�ȽϺ��㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
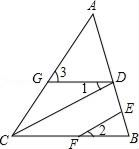
����Ŀ����ͼ����֪��CD��EF����1=��2����֤����3=��ACB���벹ȫ֤�����̣�
֤������CD��EF������ ����
���2=��DCB������ֱ��ƽ�У�ͬλ�������
�ߡ�1=��2������ ����
���1=��DCB������ ����
��GD��CB������ ����
���3=��ACB������ ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���мס������������IJ������״�����������ȫ��ͬ��С�ֱ��������1��-2���Ҵ�����������ȫ��ͬ��С�ֱ��������-1��0��2��С���ȴӼ״������ȡ��һ��С��¼��С���ϵ�����Ϊx���ٴ��Ҵ������ȡ��һ��С��¼��С���ϵ�����Ϊy�����A������Ϊ��x��y����
��1�����ñ������״ͼ�г���A���п��ܵ����ꣻ
��2�����A�ڷ���������y=![]() ͼ���ϵĸ��ʣ�
ͼ���ϵĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() �������϶�Ӧ�ĵ�ֱ�Ϊ
�������϶�Ӧ�ĵ�ֱ�Ϊ![]() ������b����С����������
������b��������������![]() ����
����![]() ��
��
��1����գ�![]() __________��
__________��![]() _____________��
_____________��![]() ___________��
___________��
��2���ֽ���A����B�͵�C�ֱ���ÿ��4����λ���ȣ�1����λ���Ⱥ�1����λ���ȵ��ٶ���������ͬʱ�����˶������˶�ʱ��Ϊt�룮
i�����壺��֪![]() Ϊ�������������㣬���������߶�
Ϊ�������������㣬���������߶�![]() ���е�Q�����۵�����M���N�պ��غϣ����������ֳ��߶�
���е�Q�����۵�����M���N�պ��غϣ����������ֳ��߶�![]() ���е�QΪ��M�͵�N���۵㣮
���е�QΪ��M�͵�N���۵㣮
���ʣ���tΪ��ֵʱ������������ǡ����һ��Ϊ����������۵㣿
ii������A�ڵ�C���ʱ�������ǵ�A���B�غϣ����Ƿ����һ������m��ʹ��![]() ��ֵ��һ��ʱ�䷶Χ�ڲ���t�ĸı���ı䣿�����ڣ����m��ֵ���������ڣ���˵�����ɣ�
��ֵ��һ��ʱ�䷶Χ�ڲ���t�ĸı���ı䣿�����ڣ����m��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�о���ʹ������ˮ�����շѣ������£�
����ÿ������ˮ������![]() ����
����![]() Ԫ/
Ԫ/![]() �շѣ�
�շѣ�
��������![]() ����������
����������![]() �����IJ��ְ�
�����IJ��ְ�![]() Ԫ/
Ԫ/![]() �շѣ�δ����
�շѣ�δ����![]() ���ְ��ٱ��շѣ�
���ְ��ٱ��շѣ�
��������![]() �������IJ��ְ�
�������IJ��ְ�![]() Ԫ/
Ԫ/![]() �շѣ�δ����
�շѣ�δ����![]() ���ְ��ڱ��շѣ�
���ְ��ڱ��շѣ�
��1������ˮ![]() ��Ӧ��ˮ��______Ԫ��(�ú�
��Ӧ��ˮ��______Ԫ��(�ú�![]() ��ʽ�ӱ�ʾ)
��ʽ�ӱ�ʾ)
��2��С�����ϸ�����ˮ![]() ����ˮ��
����ˮ��![]() Ԫ����
Ԫ����![]() ��ֵ��
��ֵ��
��3���ڣ�2���������£�С�����ߡ��������¹���ˮ��![]() Ԫ�����·���ˮ
Ԫ�����·���ˮ![]() ����
����![]() ��������
��������![]() �����·���ˮ
�����·���ˮ![]() ����
����![]() ����
����![]() ��Ϊ����ʱ����
��Ϊ����ʱ����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
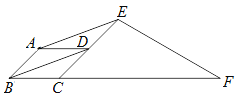
����Ŀ����ͼ����ƽ���ı���ABCD�У���ABC=45�㣬E��F�ֱ���CD��BC���ӳ����ϣ�AE��BD����EFC=30�㣬 AB=2.
��CF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ϻ��ڲ���һ�������θ���������ߣ����Խ�����ηָ�����ɸ�С�����Σ���ͼ���������ı��ε����־���ָ�����ֱ��ı��ηָ����2����3����4��С�����Σ��������ǾͿ��Խ����о������εľ����о��ı����ˣ�
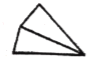
ͼ�ٱ��ָ��2��С������

ͼ�ڱ��ָ��3��С������

ͼ�۱��ָ��4��С������
��1���밴���������ַ����ֱ�ͼ�е������ν��зָ��д��ÿ�ַ������õ���С�����εĸ�����
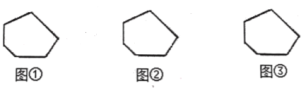
ͼ�ٱ��ָ�� ��С�����Ρ�ͼ�ڱ��ָ�� ��С�����Ρ�ͼ�۱��ָ�� ��С�����Σ�
��2����������������ַָ���ֱ�ָ�![]() ���Σ���д��ÿ�ַ������õ���С�����εĸ���(�ú�
���Σ���д��ÿ�ַ������õ���С�����εĸ���(�ú�![]() �Ĵ���ʽд�����ۼ��ɣ����ػ�ͼ)����������ͼ�١�ͼ�ڡ�ͼ�۵ķָ����
�Ĵ���ʽд�����ۼ��ɣ����ػ�ͼ)����������ͼ�١�ͼ�ڡ�ͼ�۵ķָ����![]() ���ηֱ���Ա��ָ�� �� �� ��С�����Σ�
���ηֱ���Ա��ָ�� �� �� ��С�����Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABCD���ӳ�AB��EʹBE=AB������BD��ED��EC����ED=AD��
��1����֤���ı���BECD�Ǿ��Σ�
��2������AC����AD=4��CD= 2����AC�ij���

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com