
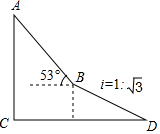
 如图,为了测量出楼房AC的高度,从距离楼底C处60$\sqrt{3}$米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1:$\sqrt{3}$的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°=$\frac{4}{5}$,cos$\frac{3}{5}$=$\frac{3}{5}$,tan53°=$\frac{4}{3}$,$\sqrt{3}$≈1.732,结果精确到0.1米)
如图,为了测量出楼房AC的高度,从距离楼底C处60$\sqrt{3}$米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1:$\sqrt{3}$的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°=$\frac{4}{5}$,cos$\frac{3}{5}$=$\frac{3}{5}$,tan53°=$\frac{4}{3}$,$\sqrt{3}$≈1.732,结果精确到0.1米) 分析 如图作BN⊥CD于N,BM⊥AC于M,先在RT△BDN中求出线段BN,在RT△ABM中求出AM,再证明四边形CMBN是矩形,得CM=BN即可解决问题.
解答 解:如图作BN⊥CD于N,BM⊥AC于M. 在Rt△BDN中,BD=30,BN:ND=1:$\sqrt{3}$,
在Rt△BDN中,BD=30,BN:ND=1:$\sqrt{3}$,
∴BN=15,DN=15 $\sqrt{3}$,
∵∠C=∠CMB=∠CNB=90°,
∴四边形CMBN是矩形,
∴CM=BN=15,BM=CN=60 $\sqrt{3}$-15 $\sqrt{3}$=45 $\sqrt{3}$,
在Rt△ABM中,tan∠ABM=$\frac{AM}{BM}$=$\frac{4}{3}$,
∴AM=60 $\sqrt{3}$,
∴AC=AM+CM=15+60 $\sqrt{3}$.
点评 本题考查解直角三角形、仰角、坡度等概念,解题的关键是添加辅助线构造直角三角形,记住坡度的定义,属于中考常考题型.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:解答题
 (1)计算:|-2|-3tan30°+(2-$\sqrt{3}$)0+$\sqrt{12}$
(1)计算:|-2|-3tan30°+(2-$\sqrt{3}$)0+$\sqrt{12}$查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
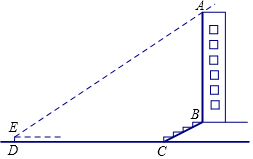 某校兴趣小组想测量一座大楼AB的高度.如图,大楼前有一段斜坡BC,已知BC的长为12米,它的坡度i=1:$\sqrt{3}$,在离C点40米的D处,用测角仪测得大楼顶端A的仰角为38°,测角仪DE的高为1.5米,求大楼AB的高度约为多少米?(结果精确到0.1米)
某校兴趣小组想测量一座大楼AB的高度.如图,大楼前有一段斜坡BC,已知BC的长为12米,它的坡度i=1:$\sqrt{3}$,在离C点40米的D处,用测角仪测得大楼顶端A的仰角为38°,测角仪DE的高为1.5米,求大楼AB的高度约为多少米?(结果精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com