
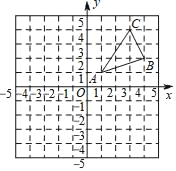
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.

(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标:
(3)在抛物线上存在点P(不与C重合),使得△APB的面积与△ACB的面积相等,求点P的坐标.
【答案】(1)y=﹣x2﹣2x+3,y=x+3;(2)点M(﹣1,2);(3)点P的坐标为:(﹣2,3)或(![]() ,﹣3)或(
,﹣3)或(![]() ,﹣3).
,﹣3).
【解析】
(1)根据抛物线的对称性求出B(﹣3,0),然后可设交点式为y=a(x﹣1)(x+3),代入(0,3)求出a即可;然后再根据B、C坐标利用待定系数法求直线BC的解析式即可;
(2)点A关于抛物线对称轴的对称点为点B,直线BC交抛物线对称轴于点M,则点M即为所求,据此即可得解;
(3)△APB的面积与△ACB的面积相等,则|yP|=yC=3,即x22x+3=±3,求解即可.
(1)∵抛物线经过A(1,0),且对称轴为直线x=﹣1,
∴点B(﹣3,0),
设抛物线的表达式为:y=a(x﹣1)(x+3),
代入C(0,3)得:3=a×(﹣1)×3,
解得:a=﹣1,
故抛物线的表达式为:y=﹣(x﹣1)(x+3)=﹣x2﹣2x+3;
由直线BC的解析式为:y=mx+n,
代入B(﹣3,0),C(0,3)得:![]() ,解得:
,解得:![]() ,
,
∴直线BC的解析式为:y=x+3;
(2)点A关于抛物线对称轴的对称点为点B(﹣3,0),直线BC交函数对称轴于点M,则点M即为所求,
∵直线BC的解析式为:y=x+3,
当x=﹣1时,y=2,
∴点M(﹣1,2);
(3)△APB的面积与△ACB的面积相等,则|yP|=yC=3,
即﹣x2﹣2x+3=±3,
当﹣x2﹣2x+3=3时,解得:x1=-2,x2=0(舍去),
当﹣x2﹣2x+3=-3时,解得:x1=![]() ,x2=
,x2=![]() ,
,
故点P的坐标为:(﹣2,3)或(![]() ,﹣3)或(
,﹣3)或(![]() ,﹣3).
,﹣3).


科目:初中数学 来源: 题型:
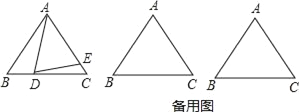
【题目】如图,已知△ABC中,AB=AC=6,BC=8,点D是BC边上的一个动点,点E在AC边上,∠ADE=∠B.设BD的长为x,CE的长为y.
(1)当D为BC的中点时,求CE的长;
(2)求y关于x的函数关系式,并写出x的取值范围;
(3)如果△ADE为等腰三角形,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春节即将来临,某企业接到一批礼品生产任务,约定这批礼品的出厂价为每件6元,按要求在20天内完成.为了按时完成任务,该企业招收了新工人,设新工人小王第x天生产的礼品数量为y件,y与x满足如下关系:y=![]() .
.
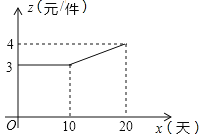
(1)小王第几天生产的礼品数量为390件?
(2)如图,设第x天生产的每件礼品的成本是z元,z与x之间的关系可用图中的函数图象来刻画.若小王第x天创造的利润为w元,求w与x之间的函数表达式,并求出第几天的利润最大?最大利润是多少元?(利润=出厂价﹣成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(﹣1,0),(3,0).对于下列命题:①b﹣2a=0;②abc<0;③a﹣2b+4c<0;④8a+c>0.其中正确的有( )
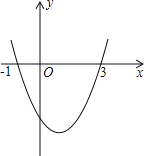
A.3个B.2个C.1个D.0个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(﹣1,0),(3,0).对于下列命题:①b﹣2a=0;②abc<0;③a﹣2b+4c<0;④8a+c>0.其中正确的有( )
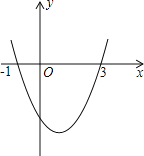
A.3个B.2个C.1个D.0个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“30元”的字样.规定:顾客在本商场同一日内,每消费满200元,就可以在箱子里先后摸出两个球(第一次摸出后不放回),商场根据两小球所标金额的和返还相应价格的购物券,可以重新在本商场消费,某顾客刚好消费200元.
(1)该顾客至少可得到_____元购物券,至多可得到_______元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于30元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)请画出△ABC关于原点对称的△A1B1C1;并写出点A1,B1,C1的坐标.
(2)请画出△ABC绕O顺时针旋转90°后的△A2B2C2,并写出点A2,B2,C2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y1=﹣x2+1,直线y2=﹣x+1,当x任取一值时,x对应的函数值分别为y1,y2.若y1≠y2,取y1,y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=2时,y1=﹣3,y2=﹣1,y1<y2,此时M=﹣3.下列判断中:①当x<0时,M=y1;②当x>0时,M随x的增大而增大;③使得M大于1的x值不存在;④使得M=![]() 的值是﹣
的值是﹣![]() 或
或![]() ,其中正确的个数有( )
,其中正确的个数有( )

A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c的对称轴为x=﹣1,且过点(![]() ,0),有下列结论:①abc>0; ②a﹣2b+4c>0;③25a﹣10b+4c=0;④3b+2c>0;其中所有正确的结论是( )
,0),有下列结论:①abc>0; ②a﹣2b+4c>0;③25a﹣10b+4c=0;④3b+2c>0;其中所有正确的结论是( )
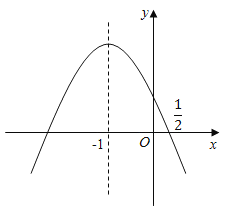
A.①③B.①③④C.①②③D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com