
【题目】如图,等腰直角△ABC和等边△AEF都是半径为R的圆的内接三角形.
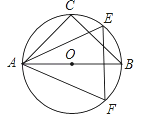
(1)求AF的长.
(2)通过对△ABC和△AEF的观察,请你先猜想谁的面积大,再证明你的猜想.
【答案】(1)AF=![]() R;(2)S△ABC<S△AEF.
R;(2)S△ABC<S△AEF.
【解析】
(1)连接OF,过O作OG⊥AF于G,在直角△OGF中,利用三角函数即可求解;
(2)根据外接圆的半径是R,即可求得等腰直角△ABC和等边△AEF的面积,即可作出比较.
(1)如图,连接OF,过O作OG⊥AF于G,OF=R,
又∵△AEF为等边三角形,
∴∠AOF=120°,
∴∠GOF=60°,
在Rt△GOF中,sin∠GOF=![]() ,即sin60°=
,即sin60°=![]() ,
,
∴GF=![]() R,
R,
∴AF=2GF=![]() R;
R;
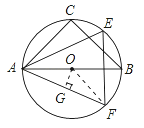
(2)S△ABC<S△AEF,理由如下:
∵直角△ABC是等腰直角三角形.
∴AB=2R,
∴AC=![]() R,
R,
∴S△ABC=R2,
![]() ,
,![]() ,
,![]() ,
,
∴S△ABC<S△AEF.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】二次函数的图象经过A(4,0),B(0,﹣4),C(2,﹣4)三点.
(1)求这个函数的解析式;
(2)求函数图顶点的坐标;
(3)求抛物线与坐标轴的交点围成的三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
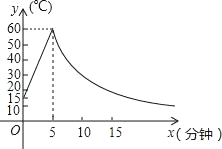
【题目】如图为某种材料温度y(℃)随时间x(min)变化的函数图象.已知该材料初始温度为15℃,温度上升阶段y与时间x成一次函数关系,且在第5分钟温度达到最大值60℃后开始下降;温度下降阶段,温度y与时间x成反比例关系.
(1)分别求该材料温度上升和下降阶段,y与x间的函数关系式;
(2)根据工艺要求,当材料的温度高于30℃时,可以进行产品加工,问可加工多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB为⊙O的直径,点C、D在⊙O上,且BC=6cm,AC=8cm,∠ABD=45°.

(1)求BD的长;
(2)求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
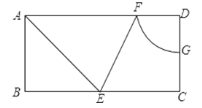
【题目】如图,矩形ABCD中,BC=2AB=4,AE平分∠BAD交边BC于点E,∠AEC的分线交AD于点F,以点D为圆心,DF为半径画圆弧交边CD于点G,则![]() 的长为________
的长为________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系中有两点A(0,1),B(﹣1,0),动点P在反比例函数y=![]() 的图象上运动,当线段PA与线段PB之差的绝对值最大时,点P的坐标为_____.
的图象上运动,当线段PA与线段PB之差的绝对值最大时,点P的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线M:y=ax2+bx+c(a≠0)经过A(﹣1,0),且顶点坐标为B(0,1).
(1)求抛物线M的函数表达式;
(2)设F(t,0)为x轴正半轴上一点,将抛物线M绕点F旋转180°得到抛物线M1.
①抛物线M1的顶点B1的坐标为 ;
②当抛物线M1与线段AB有公共点时,结合函数的图象,求t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与x轴交于点A,与反比例函数y=![]() (x>0)的图象交于点B(2,n),过点B作BC⊥x轴于点C,点P(3n﹣4,1)是该反比例函数图象上的一点,且∠PBC=∠ABC,求反比例函数和一次函数的表达式.
(x>0)的图象交于点B(2,n),过点B作BC⊥x轴于点C,点P(3n﹣4,1)是该反比例函数图象上的一点,且∠PBC=∠ABC,求反比例函数和一次函数的表达式.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com