
����Ŀ�����Ķ����в��ϣ��������Ӧ������
���������Ҷ���
������Al-Biruni��973��~1050�꣩�������б����˰��������Ҷ��������ݣ�������1964�����Al-Biruni�뱾�����˶��İ桶������ȫ��������һ����ǰ����µ����Ҷ�����
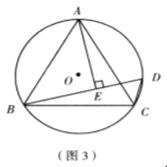
���������Ҷ�������ͼ1��AB��BC��![]() �������ң�������ABC��Բ��һ�����ң���BC>AB��M��
�������ң�������ABC��Բ��һ�����ң���BC>AB��M��![]() ���е㣬���M��BC�������ߵĴ���D������ABC���е㣬��CD=AB+BD��
���е㣬���M��BC�������ߵĴ���D������ABC���е㣬��CD=AB+BD��
���������á��س�����֤��CD=AB+BD�IJ���֤�����̣�
֤������ͼ����CB�Ͻ�ȡCG=AB������MA��MB��MC��MG����M��![]() ���е㣬 ��MA=MC ������
���е㣬 ��MA=MC ������
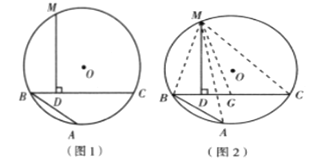
����1���밴�������֤��˼·��д����֤����ʣ�ಿ�֣�
��2����գ���ͼ��3������֪�ȱߡ�ABC�ڽ���![]() ��AB=2��DΪԲ��һ�㣬��ABD=45�㣬AE��BD���E�����BDC���ܳ��� ��
��AB=2��DΪԲ��һ�㣬��ABD=45�㣬AE��BD���E�����BDC���ܳ��� ��
���𰸡���1�������������2��2+2![]() .
.
��������
��1����ͼ2����CB�Ͻ�ȡCG=AB������MA��MB��MC��MG������֤����MBA�ա�MGC��SAS���������ó�MB=MG�������õ��������ε����ʵó�BD=GD�����ɵó��𰸣�
��2����ͼ3����ȡBF=CD������AF��AD��CD������֤����ABF��ACD��SAS���������ó�AF=AD���Լ�CD+DE=BE���������DE�ij����ɵó��𰸣�
��1��֤������ͼ2����CB�Ͻ�ȡCG=AB������MA��MB��MC��MG��
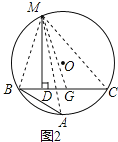
��M��![]() ���е㣬
���е㣬
��MA=MC��
����MBA����MGC��
�� ��
��
���MBA�ա�MGC��SAS����
��MB=MG��
�֡�MD��BC��
��BD=GD��
��DC=GC+GD=AB+BD��
��2���⣺��ͼ3����ȡBF=CD������AF��AD��CD��
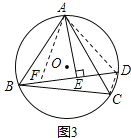
������ɵã�AB=AC����ABF=��ACD��
����ABF����ACD��
��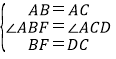 ��
��
���ABF��ACD��SAS����
��AF=AD��
��AE��BD��
��FE=DE����CD+DE=BE��
�ߡ�ABD=45����AB=2
��BE=![]() ��
��
��BD+CD=2BE=2![]() ��
��
�ߡ�ABC�ǵȱ������Σ�
��BC=AB=2��
����BDC���ܳ���2+2![]() ��
��


 Ӧ�����������Ĵ���ѧ������ϵ�д�
Ӧ�����������Ĵ���ѧ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� �����л�ʫ�ʣ�Ѱ�Ļ�����Ʒ����֮������ijУ�ٰ����조�й�ʫ�ʴ�ᡱ����ѡ�κ���50��ѧ���μӾ�������50��ѧ��ͬʱĬд50��ʫ�ʣ���ÿ��ȷĬд��һ��ʫ�ʵ�2�֣����ݲ��Գɼ����Ƴ�����Ƶ���ֲ����Ͳ���Ƶ���ֲ�ֱ��ͼ��ͼ����
����ͼ��������и��⣺
��1��������a��ֵΪ ����λ���ڵ� �飻
��Ƶ���ֲ�ֱ��ͼ����������
��2�������Գɼ�������80��Ϊ���㣬�β��Ե��������Ƕ��٣�
��3����5��10��ͬѧ�У���4����ͬѧ���ֽ���10��ͬѧƽ���ֳ�������жԿ���ϰ����4����ͬѧÿ������ˣ���С����Сǿ������ͬѧ�ܷ���ͬһ��ĸ��ʣ�
��� | �ɼ�x�� | Ƶ���������� |
��1�� | 50��x��60 | 6 |
��2�� | 60��x��70 | 8 |
��3�� | 70��x��80 | 14 |
��4�� | 80��x��90 | a |
��5�� | 90��x��100 | 10 |

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ϊ�ӿ�������彨�裬���������Ҹ�Ѧ�ǣ���A��B�����ׯ������ȫ��Ľ�.����Ԥ�㣬����һ��A��������ׯ��һ��B��������ׯ�����ʽ�300��Ԫ����������2��A���ׯ��5��B���ׯ��Ͷ���ʽ�1140��Ԫ.
(1)����һ��A��������ׯ��һ��B��������ׯ������ʽ�ֱ��Ƕ�����Ԫ?
(2)����3��A��������ׯ��6��B��������ׯ�ĸĽ������ʽ������Ԫ?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ���ڵ�����ֱ�����ཻ��ƽ������λ�ù�ϵ

��1����ͼa����AB��CD����P��AB��CD�ⲿ�����С�B����BOD�������BOD�ǡ�POD����ǣ��ʡ�BOD����BPD+��D���á�BPD����B����D������P�Ƶ�AB��CD�ڲ�����ͼb�����Ͻ����Ƿ��������������˵�����ɣ��������������BPD����B����D֮���к�������ϵ����֤����Ľ��ۣ�
��2����ͼb�У���ֱ��AB�Ƶ�B��ʱ�뷽����תһ���ǶȽ�ֱ��CD�ڵ�Q����ͼc�����BPD����B����D����BQD֮���к�������ϵ��������֤����
��3�����ݣ�2���Ľ�����ͼd�С�A+��B+��C+��D+��E+��F�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��������y=ax2+bx+c��������ֱ��ڵ�A��0��6����B��6��0����C����2��0������P���߶�AB�Ϸ��������ϵ�һ�����㣮
��1���������ߵĽ���ʽ��
��2������P�˶���ʲôλ��ʱ����PAB����������ֵ��
��3������P��x��Ĵ��ߣ����߶�AB�ڵ�D���ٹ���P��PE��x�ύ�������ڵ�E������DE�������Ƿ���ڵ�Pʹ��PDEΪ����ֱ�������Σ������ڣ������P�����ꣻ�������ڣ�˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҹ���һ������ȱˮ�Ĺ��ң�Ϊ�˼�ǿ����Ľ�ˮ��ʶ��ij���ƶ���������ˮ�շѱ���ÿ��ÿ�µ���ˮ������6��ʱ��ˮ��Ϊÿ��2Ԫ������6��ʱ�������IJ��ְ�ÿ��3Ԫ�շѣ�����ij������5�·���ˮx�֣�Ӧ��ˮ��yԪ��
��1����0��x��6����д��y��x�ĺ�����ϵʽ��
��2����x��6����д��y��x�ĺ�����ϵʽ��
��3����ͬһ����ϵ�£�������������������ͼ��
��4������û���������½�ˮ��27Ԫ����ô����¸û����˶��ٶ�ˮ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij�ִ������������У��ڵ�![]() ����õ���
����õ���![]() �ڱ�ƫ��
�ڱ�ƫ��![]() �����ϣ��ִ���ÿСʱ
�����ϣ��ִ���ÿСʱ![]() ������ٶȺ���
������ٶȺ���![]() Сʱ����
Сʱ����![]() ��õ���
��õ���![]() �ڱ�ƫ��
�ڱ�ƫ��![]() �����ϣ����ִ��������
�����ϣ����ִ��������![]() ����������ʱ���ִ�������ж�Զ���������ȷ��
����������ʱ���ִ�������ж�Զ���������ȷ��![]() ����ο����ݣ�
����ο����ݣ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�Ƕ��κ���y=ax2+bx+c��a��b��c�dz�����a��0��ͼ���һ���֣���x��Ľ���A�ڵ㣨2��0���ͣ�3��0��֮�䣬�Գ�����x=1����������˵������ab��0����2a+b=0����3a+c��0����a+b��m��am+b����mΪʵ������������1��x��3ʱ��y��0��������ȷ���ǣ�������

A. �٢ڢ� B. �٢ڢ� C. �ڢۢ� D. �ۢܢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲�����ݱ������������⣺
x | 0 | 1 | 2 |
ax2 | 0 | 1 | 4 |
ax2+bx+c | ��3 | -4 | ��3 |
��l����a��b��c��ֵ��
��2������ͼ��ֱ������ϵ�л�������y=ax2+bx+c��ͼ������ͼ��ֱ��д����xȡʲôʵ��ʱ������ʽax2+bx+c����3������
��3����ͼ����x����������������ηֱ�ΪA��B����y�ύ��ΪC�����������������Բ�İ뾶��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com