
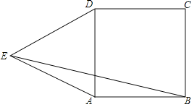
【题目】如图,![]() 为正方形
为正方形![]() 外一点,
外一点,![]() ,
,![]() ,则
,则![]() 的长为________.
的长为________.
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AD是△ABC的中线,AE∥BC,射线BE交AD于点F,交⊙O于点G,点F是BE的中点,连接CE.
(1)求证:四边形ADCE为平行四边形;
(2)若BC=2AB,求证: ![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读情境:在综合实践课上,同学们探究“全等的等腰直角三角形图形变化问题”
如图1,![]() ,其中
,其中![]() ,
,![]() ,此时,点
,此时,点![]() 与点
与点![]() 重合,
重合,
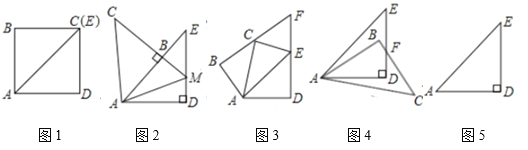
操作探究1:(1)小凡将图1中的两个全等的![]() 和
和![]() 按图2方式摆放,点
按图2方式摆放,点![]() 落在
落在![]() 上,
上,![]() 所在直线交
所在直线交![]() 所在直线于点
所在直线于点![]() ,连结
,连结![]() ,求证:
,求证:![]() .
.
操作探究2:(2)小彬将图1中的![]() 绕点
绕点![]() 按逆时针方向旋转角度
按逆时针方向旋转角度![]()
![]() ,然后,分别延长
,然后,分别延长![]() ,
,![]() ,它们相交于点
,它们相交于点![]() .如图3,在操作中,小彬提出如下问题,请你解答:
.如图3,在操作中,小彬提出如下问题,请你解答:
①![]() 时,求证:
时,求证:![]() 为等边三角形;
为等边三角形;
②当![]() __________时,
__________时,![]() .(直接回答即可)
.(直接回答即可)
操作探究3:(3)小颖将图1中的![]() 绕点
绕点![]() 按顺时针方向旋转角度
按顺时针方向旋转角度![]()
![]() ,线段
,线段![]() 和
和![]() 相交于点
相交于点![]() ,在操作中,小颖提出如下问题,请你解答:
,在操作中,小颖提出如下问题,请你解答:
①如图4,当![]() 时,直接写出线段
时,直接写出线段![]() 的长为_________.
的长为_________.
②如图5,当旋转到点![]() 是边
是边![]() 的中点时,直接写出线段
的中点时,直接写出线段![]() 的长为____________.
的长为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了促进“足球进校园”活动的开展,某市举行了中学生足球比赛活动现从A,B,C三支获胜足球队中,随机抽取两支球队分别到两所边远地区学校进行交流.
(1)请用列表或画树状图的方法(只选择其中一种),表示出抽到的两支球队的所有可能结果;
(2)求出抽到B队和C队参加交流活动的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,抛物线
,抛物线![]() 经过点
经过点![]() 、
、![]() ,且与
,且与![]() 轴的另一交点为
轴的另一交点为![]() ,连接
,连接![]() .
.
(1)求抛物线的解析式;
(2)点![]() 在线段
在线段![]() 上方的抛物线上,连接
上方的抛物线上,连接![]() 、
、![]() ,若
,若![]() 和
和![]() 面积满足
面积满足![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)如图2,![]() 为
为![]() 中点,设
中点,设![]() 为线段
为线段![]() 上一点(不含端点),连接
上一点(不含端点),连接![]() 。一动点
。一动点![]() 从
从![]() 出发,沿线段
出发,沿线段![]() 以每秒1个单位的速度运动到
以每秒1个单位的速度运动到![]() ,再沿着线段
,再沿着线段![]() 以每秒
以每秒![]() 个单位的速度运动到
个单位的速度运动到![]() 后停止。当点
后停止。当点![]() 的坐标是多少时,点
的坐标是多少时,点![]() 在整个运动过程中用时最少?最少时间是几秒?
在整个运动过程中用时最少?最少时间是几秒?
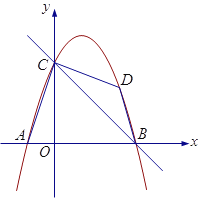

图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
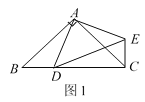
【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=_______度;
(2)如图2如果∠BAC=60°,则∠BCE=______度;
(3)设∠BAC=![]() ,∠BCE=
,∠BCE=![]() .
.
①如图3,当点D在线段BC上移动,则![]() 之间有怎样的数量关系?请说明理由;
之间有怎样的数量关系?请说明理由;
②当点D在直线BC上移动,请直接写出![]() 之样的数量关系,不用证明。
之样的数量关系,不用证明。

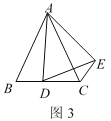
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在日历上,我们可以发现其中某些数满足一定的规律,如图是2012年8月份的日历.我们任意选择其中所示的方框部分,将每个方框部分中4个位置上的数交又相乘,再相减,例如:7×13-6×14=7,17×23-16×24=7,不难发现,结果都是7.
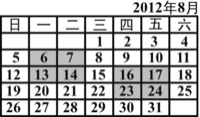
①请你再选择一个类似的部分试一试,看看是否符合这个规律;
②请你利用整式的运算对以上的规律加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
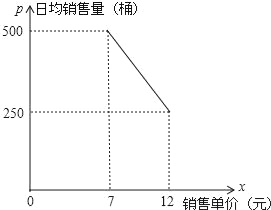
【题目】无锡市新区某桶装水经营部每天的房租、人员工资等固定成本为250元,每桶水的进价是5元,规定销售单价不得高于12元/桶,也不得低于7元/桶,调查发现日均销售量p(桶)与销售单价x(元)的函数图象如图所示.
(1)求日均销售量p(桶)与销售单价x(元)的函数关系;
(2)若该经营部希望日均获利1350元,那么销售单价是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com