
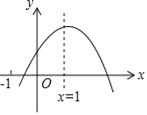
【题目】已知二次函数y=ax2+bx+c的图象如图所示,给出下列结论:①abc>0;②a﹣b+c<0;③2a+b﹣c<0;④4a+2b+c>0,⑤若点(﹣![]() ,y1)和(
,y1)和(![]() ,y2)在该图象上,则y1>y2.其中正确的结论是_____(填入正确结论的序号)
,y2)在该图象上,则y1>y2.其中正确的结论是_____(填入正确结论的序号)
【答案】②③④
【解析】解:∵抛物线开口向下,
∴a<0,
∵对称轴在y轴右边,
∴b>0,
∵抛物线与y轴的交点在x轴的上方,
∴c>0,
∴abc<0,故①错误;
∵二次函数y=ax2+bx+c图象可知,当x=﹣1时,y<0,
∴a﹣b+c<0,故②正确;
∵二次函数图象的对称轴是直线x=1,c>0,
∴﹣![]() =1,
=1,
∴2a+b=0,
∴2a+b<c,
∴2a+b﹣c<0,故③正确;
∵二次函数y=ax2+bx+c图象可知,当x=2时,y>0,
∴4a+2b+c>0,故④正确;
∵二次函数图象的对称轴是直线x=1,
∴抛物线上x=﹣![]() 时的点与当x=
时的点与当x=![]() 时的点对称,
时的点对称,
∵x>1,y随x的增大而减小,
∴y1<y2,故⑤错误;
故答案为:②③④.


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】已知常数a(a是整数)满足下面两个要求:
①关于x的一元二次方程ax2+3x﹣1=0有两个不相等的实数根;
②反比例函数y=![]() 的图象在二,四象限.
的图象在二,四象限.
(1)求a的值;
(2)在所给直角坐标系中用描点法画出y=![]() 的图象,并根据图象写出:
的图象,并根据图象写出:
当x>4时,y的取值范围 ;
当y<1时,x的取值范围是.
查看答案和解析>>
科目:初中数学 来源: 题型:
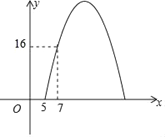
【题目】某商场经调研得出某种商品每天的利润y(元)与销售单价x(元)之间满足关系:y=ax2+bx﹣75,其图象如图所示.
(1)求a与b的值;
(2)销售单价为多少元时,该种商品每天的销售利润最大?最大利润是多少元?(参考公式:当x=![]() 时,二次函数y=ax2+bx+c(a≠0)有最小(大)值)
时,二次函数y=ax2+bx+c(a≠0)有最小(大)值)
(3)销售单价定在多少时,该种商品每天的销售利润为21元?结合图象,直接写出销售单价定在什么范围时,该种商品每天的销售利润不低于21元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=14.5米,NF=0.2米.设太阳光线与水平地面的夹角为α,当α=56.3°时,测得楼房在地面上的影长AE=10米,现有一只小猫睡在台阶的NF这层上晒太阳.

(1)求楼房的高度约为多少米?
(2)过了一会儿,当α=45°时,问小猫能否还晒到太阳?请说明理由.(参考数据:sin56.3°≈0.83,cos56.3°≈0.55,tan56.3°≈1.5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年暑假,小丽爸爸的同事送给她爸爸一张北京故宫的门票,她和哥哥两人都很想去参观,可门票只有一张.读九年级的哥哥想了一个办法,他拿了八张扑克牌,将数字为1,2,3,5的四张牌给小丽,将数字为4,6,7,8的四张牌留给自己,并按如下游戏规则进行:小利哥哥从各自的四张牌中随机抽出一张,然后将抽出的两张扑克牌上的数字相加,如果和为偶数,和小丽去;如果和为奇数,则哥哥去.
(1)请用画树状图或列表的方法求小丽去北京故宫参观的概率;
(2)哥哥设计的游戏规则公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2+ax+b=0(b≠0)与x2+cx+d=0都有实数根,若这两个方程有且只有一个公共根,且ab=cd,则称它们互为“同根轮换方程”.如x2-x-6=0与x2-2x-3=0互为“同根轮换方程”.
(1)若关于x的方程x2+4x+m=0与x2-6x+n=0互为“同根轮换方程”,求m的值;
(2)已知方程①:x2+ax+b=0和方程②:x2+2ax+![]() b=0,p、q分别是方程①和方程②的实数根,且p≠q,b≠0.试问方程①和方程②是否能互为“同根轮换方程”?如果能,用含a的代数式分别表示p和q;如果不能,请说明理由.
b=0,p、q分别是方程①和方程②的实数根,且p≠q,b≠0.试问方程①和方程②是否能互为“同根轮换方程”?如果能,用含a的代数式分别表示p和q;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
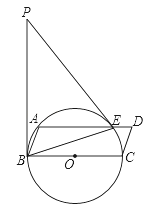
【题目】如图,BC为⊙O的直径,A为⊙O上的点,以BC、AB为边作ABCD,⊙O交AD于点E,连结BE,点P为过点B的⊙O的切线上一点,连结PE,且满足∠PEA=∠ABE.
(1)求证:PB=PE;
(2)若sin∠P=![]() , 求
, 求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:
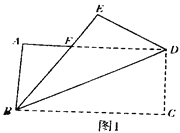
在综合实践课上,张老师让同学们以“矩形的折叠”为主题开展数学活动,张老师拿着一张矩形纸片ABCD,其中AB=acm, AD=bcm, 如图1,先沿对角线BD折叠,点C落在点E的位置,BE交AD于点F.
操作发现:
(1)“奋进”小组发现与BF的长度一定相等的线段是哪一条;
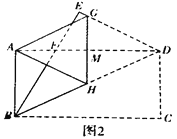
(2)如图2.“雄鹰”小组将图1再折叠一次,使点D与点A重合,得到折痕GH,GH交AD于点M,发现△DGH是等腰三角形,请你证明这个结论;
实践探究:
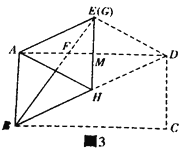
(3)“创新”小组将自己准备的矩形纸片按照(2)中“雄鹰”小组的作法操作,发现点E和点G重合,,如图3,试探究“创新”小组准备的矩形纸片中a与b满足的数量关系;
(4)”爱心”小组在其他小组的基础上提出问题:当a与b满足什么关系时,点G是DE的中点?请你直接出a与b满足的关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com