
 如图所示,△ABC中,D点在AC上,E点在BC上,且满足△ABD≌△EBD,△DBE≌△DCE,求∠A和∠C的度数.
如图所示,△ABC中,D点在AC上,E点在BC上,且满足△ABD≌△EBD,△DBE≌△DCE,求∠A和∠C的度数.  名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
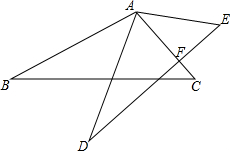 在讲完全等三角形后,数学老师王老师布置了一道数学题:如图所示,已知△ABC≌△ADE,其中∠CAE=40°,∠C=50°,则DE与AC有何位置关系?请说明理由.
在讲完全等三角形后,数学老师王老师布置了一道数学题:如图所示,已知△ABC≌△ADE,其中∠CAE=40°,∠C=50°,则DE与AC有何位置关系?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 抛物线y=-2x2+3x+1的对称轴是直线x=$\frac{3}{4}$ | |
| B. | 点A(3,0)不在抛物线y=x2-2x-3的图象上 | |
| C. | 二次函数y=(x+2)2-2的顶点坐标是(-2,-2) | |
| D. | 函数y=2x2+4x-3的图象的最低点在(-1,-5) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com