
【题目】如图,在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.
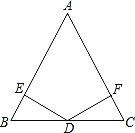
(1)求证:△BED≌△CFD;
(2)若∠A=60°,BE=2,求△ABC的周长.
【答案】(1)证明见解析;(2)24
【解析】
试题分析:(1)根据DE⊥AB,DF⊥AC,AB=AC,求证∠B=∠C.再利用D是BC的中点,求证△BED≌△CFD即可得出结论.
(2)根据AB=AC,∠A=60°,得出△ABC为等边三角形.然后求出∠BDE=30°,再根据题目中给出的已知条件即可算出△ABC的周长.
试题解析:(1)∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°,
∵AB=AC,
∴∠B=∠C(等边对等角).
∵D是BC的中点,
∴BD=CD.
在△BED和△CFD中,
 ,
,
∴△BED≌△CFD(AAS).
∴DE=DF
(2)∵AB=AC,∠A=60°,
∴△ABC为等边三角形.
∴∠B=60°,
∵∠BED=90°,
∴∠BDE=30°,
∴BE=![]() BD,
BD,
∵BE=2,
∴BD=4,
∴BC=2BD=8,
∴△ABC的周长为24.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】阅读材料:如图(一),△ABC的周长为![]() ,内切圆O的半径为r,连结OA、OB、OC,△ABC被划分为三个小三角形,用S△ABC表示△ABC的面积
,内切圆O的半径为r,连结OA、OB、OC,△ABC被划分为三个小三角形,用S△ABC表示△ABC的面积
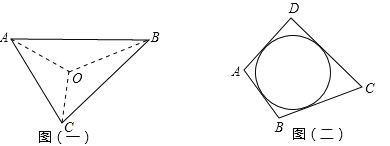
∵ S△ABC=S△OAB+S△OBC+S△OCA
又∵S△OAB=![]() ,S△OBC=
,S△OBC=![]() ,S△OCA =
,S△OCA =![]()
∴S△ABC=![]() +
+![]() +
+![]() =
=![]() (可作为三角形内切圆半径公式)
(可作为三角形内切圆半径公式)
(1)理解与应用:利用公式计算边长分为5、12、13的三角形内切圆半径;
(2)类比与推理:若四边形ABCD存在内切圆(与各边都相切的圆,如图(二))且面积为S,各边长分别为a、b、c、d,试推导四边形的内切圆半径公式;
(3)拓展与延伸:若一个n边形(n为不小于3的整数)存在内切圆,且面积为S,各边长分别为a1、a2、a3、…、an,合理猜想其内切圆半径公式(不需说明理由).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上一点 A,一只蚂蚁从 A 出发爬了 4 个单位长度到了原点,则点 A 所表 示的数是( )
A. 4 B. ﹣4 C. ±8 D. ±4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,任何一个三角形的三条内角平分线相交于一点,如图,若△ABC 的三条内角平分线相交于点I,过I作DE⊥AI分别交AB、AC于点D、E.

(1)请你通过画图、度量,填写右上表(图画在草稿纸上,并尽量画准确)
(2)从上表中你发现了∠BIC与∠BDI之间有何数量关系,请写出来,并说明其中的道理.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 要了解我市九年级学生的身高,应采用普查的方式;
B. 若甲队成绩的方差为5,乙队成绩的方差为3,则甲队成绩不如乙队成绩稳定;
C. 如果明天下雨的概率是99%,那么明天一定会下雨;
D. 一组数据4,6,7,6,7,8,9的中位数和众数都是6.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店上月的营业额是a万元,本月比上月增长15%,则本月营业额是( )
A. 15%(a+1)万元 B. 15% a万元 C. (1+15%)a万元 D. (1+15%)2a万元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一条船从海岛A出发,以25海里/时的速度向正东方向航行,2小时后到达海岛B处,从A、B望灯塔C,测得∠DBC=68°,∠DAC=34°,求海岛B与灯塔C的距离.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com