
【题目】(1)计算:
①![]()
② -10 - (-31)
③1÷(﹣![]() )×
)×![]() ;
;
④(-2)2×5+(-2)3÷4
⑤![]()
(2)比较大小
①1.5与4 ②2与-7
③![]() 与
与![]() ④
④ ![]() 与
与![]()
(3)用简便方法计算:
①![]()
②![]()
【答案】(1)①0;②21;③-![]() ;④18;⑤37;(2)①1.5<4;②2>-7;③
;④18;⑤37;(2)①1.5<4;②2>-7;③![]() ;④-
;④-![]() >-0.4;(3)①
>-0.4;(3)①![]() ;②-7199.
;②-7199.
【解析】
(1)①根据任何数和零相乘都得0;
②根据有理数的减法可以解答本题;
③根据有理数的除法和乘法可以解答本题;
④根据有理数的乘法、除法和加法可以解答本题;
⑤根据乘法分配律可以解答本题.
(2)①根据正数的大小关系,可得答案;
②根据有理数比较大小,正数大于负数,可得答案;
③根据两个负数比较大小,绝对值大的数反而小,可得答案;
④根据两个负数比较大小,绝对值大的数反而小,可得答案.
(3)①原式逆用乘法分配律计算即可得到结果;
②原式变形后,利用乘法分配律计算即可得到结果.
(1)
①(-13)×(-15)×0×(-901)
=0;
②-10-(-31)
=-10+31
=21;
③1÷(﹣![]() )×
)×![]()
=1×(﹣![]() )×
)×![]()
=-![]() ;
;
④)(-2)2×5+(-2)3÷4
=4×5+(-8)÷4
=20+(-2)
=18;
⑤![]()
=![]()
=-12+40+9
=37.
(2)①1.5<4,
②正数大于负数,
∴2>-7;
③这是两个负数比较大小,先求他们的绝对值,
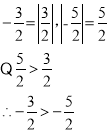
④这是两个负数比较大小,先求他们的绝对值,
|-0.4|=0.4,|-![]() |=0.2.
|=0.2.
∵0.4>0.2,
∴-![]() >-0.4.
>-0.4.
(3)①原式=![]()
②原式=![]()


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(10,0),以OA为直径在第一象限内作半圆C,点B是该半圆周上的一动点,连结OB、AB,并延长AB至点D,使DB=AB,过点D作x轴垂线,分别交x轴、直线OB于点E、F,点E为垂足,连结CF.

(1)当∠AOB=30°时,求弧AB的长;
(2)当DE=8时,求线段EF的长;
(3)在点B运动过程中,是否存在以点E、C、F为顶点的三角形与△AOB相似,若存在,请求出此时点E的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,王老师站在湖边度假村的景点A处,观察到一只水鸟由岸边D处飞向湖中小岛C处,点A到DC所在水平面的距离AB是15米,观测水鸟在点D和点C处时的俯角分别为53°和11°,求C、D两点之间距离.(精确到0.1.参考数据sin53°≈0.80,cos53°≈0.60,tan53°≈1.33,sin11°≈0.19,cos11°≈0.98,tan11°≈0.19)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家规定“中小学生每天在校体育活动时间不低于1小时”.为此,某市就“每天在校体育活动时间”的问题随机抽样调查了321名初中学生.根据调查结果将学生每天在校体育活动时间t(小时)分成![]() ,
,![]() ,
,![]() ,
,![]() 四组,并绘制了统计图(部分).
四组,并绘制了统计图(部分).
![]() 组:
组:![]() 组:
组:![]() 组:
组:![]() 组:
组:![]()

请根据上述信息解答下列问题:
(1)![]() 组的人数是 ;
组的人数是 ;
(2)本次调查数据的中位数落在 组内;
(3)若该市约有12840名初中学生,请你估算其中达到国家规定体育活动时间的人数大约有多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,∠BAD=60°
(1) 如图1,点E为线段AB的中点,连接DE、CE.若AB=4,求线段EC的长
(2) 如图2,M为线段AC上一点(不与A、C重合),以AM为边向上构造等边三角形AMN,线段MN与AD交于点G,连接NC、DM,Q为线段NC的中点,连接DQ、MQ,判断DM与DQ的数量关系,并证明你的结论
(3) 在(2)的条件下,若AC=![]() ,请你直接写出DM+CN的最小值
,请你直接写出DM+CN的最小值

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】生活与数学
日 | 一 | 二 | 三 | 四 | 五 | 六 |
1 | 2 | 3 | 4 | 5 | 6 | |
7 | 8 | 9 | 10 | 11 | 12 | 13 |
14 | 15 | 16 | 17 | 18 | 19 | 20 |
21 | 22 | 23 | 24 | 25 | 26 | 27 |
(1)姆同学在某月的日历上圈出2×2个数,正方形的方框内的四个数的和是48,那么这四个数是_______.
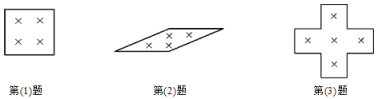
(2)丽也在上面的日历上圈出2×2个数,斜框内的四个数的和是46,则它们分别是_____.
(3)莉也在日历上圈出5个数,呈十字框形,它们的和是55,则中间的数是______.
(4)某月有5个星期日的和是75,则这个月中最后一个星期日是______号?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠BAC=α,点P是△ABC内一点,且![]() .连接PB,试探究PA,PB,PC满足的等量关系.
.连接PB,试探究PA,PB,PC满足的等量关系.
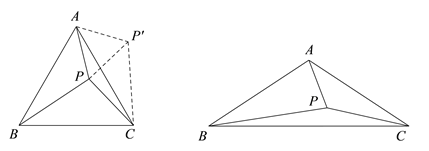
图1 图2
(1)当α=60°时,将△ABP绕点A逆时针旋转60°得到![]() ,连接
,连接![]() ,如图1所示.
,如图1所示.
由![]() ≌
≌![]() 可以证得
可以证得![]() 是等边三角形,再由
是等边三角形,再由![]() 可得∠APC的大小为 度,进而得到
可得∠APC的大小为 度,进而得到![]() 是直角三角形,这样可以得到PA,PB,PC满足的等量关系为 ;
是直角三角形,这样可以得到PA,PB,PC满足的等量关系为 ;
(2)如图2,当α=120°时,请参考(1)中的方法,探究PA,PB,PC满足的等量关系,并给出证明;
(3)PA,PB,PC满足的等量关系为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
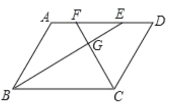
【题目】如图,在□ABCD中,∠ABC,∠BCD的平分线分别交AD于点E,F,BE,CF相交于点G.
(1)求证:BE⊥CF;
(2)若AB=a,CF=b,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
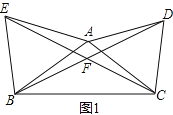
【题目】已知△ABC,以AC为边在△ABC外作等腰△ACD,其中AC=AD
(1) 如图1,若AB为边在△ABC外作△ABE,AB=AE,∠DAC=∠EAB=60°,求∠BFC的度数
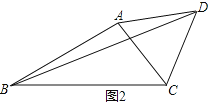
(2) 如图2,∠ABC=α,∠ACD=β,BC=6,BD=8
① 若α=30°,β=60°,AB的长为
② 若改变α、β的大小,但α+β=90°,求△ABC的面积
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com