
分析 (1)整理方程组为一般式,再利用加减消元法求解可得.
(2)分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
解答 解:(1)原方程组变形为$\left\{\begin{array}{l}{3x-y=8}&{①}\\{3x-5y=-20}&{②}\end{array}\right.$
①-②,得4y=28,
∴y=7,
把y=7代入①得,3x-7=8,
所以x=5,
所以原方程组的解是$\left\{\begin{array}{l}x=5\\ y=7\end{array}\right.$;
(2)解不等式①得,x<1,
解不等式②得,x≥-5,
在数轴上表示不等式①,②的解集,如图
所以,不等式组的解集是-5≤x<1.
点评 本题考查的是解二元一次方程组和一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.


科目:初中数学 来源: 题型:解答题
| (1)$\frac{4}{13}+({\frac{7}{13}-\frac{5}{13}})$ | (2)$\frac{7}{9}-\frac{5}{12}+\frac{5}{18}$ | (3)$\frac{11}{15}-({\frac{4}{5}-\frac{4}{3}})$ |
| (4)$2\frac{1}{3}-({\frac{1}{6}+0.75})$ | (5)3.74+$1\frac{4}{9}+2.26+1\frac{5}{9}$ | (6)$\frac{15}{14}×\frac{21}{10}÷\frac{3}{4}$. |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
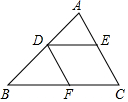 如图,DE∥BC,DF∥AC,则下列比例式中正确的是( )
如图,DE∥BC,DF∥AC,则下列比例式中正确的是( )| A. | $\frac{AD}{DB}=\frac{DE}{BC}$ | B. | $\frac{AE}{EC}=\frac{BF}{FC}$ | C. | $\frac{DF}{AC}=\frac{DE}{BC}$ | D. | $\frac{EC}{AC}=\frac{BF}{BC}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
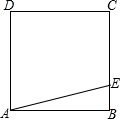 有一块边长为40米的正方形绿地ABCD,如图所示,在绿地旁边E处有健身器材,BE=9米.由于居住在A处的居民去健身践踏了绿地,小明想在A处树立一个标牌“少走■米,踏之何忍”.请你计算后帮小明在标牌的■处填上适当的数.
有一块边长为40米的正方形绿地ABCD,如图所示,在绿地旁边E处有健身器材,BE=9米.由于居住在A处的居民去健身践踏了绿地,小明想在A处树立一个标牌“少走■米,踏之何忍”.请你计算后帮小明在标牌的■处填上适当的数.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
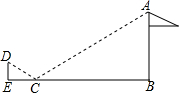 如图,为了测量旗杆AB的高度,小凡在距旗杆底部B点10.8米的C点处放置了一面镜子,当小凡行走到与BC位于同一直线的E点处时,恰好能从镜子中观察到旗杆顶部的A点.已知小凡眼睛所在的D点离地面的高度是1.6米,CE=2.7米,则旗杆AB的高度是( )
如图,为了测量旗杆AB的高度,小凡在距旗杆底部B点10.8米的C点处放置了一面镜子,当小凡行走到与BC位于同一直线的E点处时,恰好能从镜子中观察到旗杆顶部的A点.已知小凡眼睛所在的D点离地面的高度是1.6米,CE=2.7米,则旗杆AB的高度是( )| A. | 6.4米 | B. | 7.2米 | C. | 8米 | D. | 9.6米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
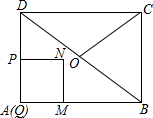 如图1,在矩形ABCD中,AB=4,BC=3,点O为对角线BD的中点,点P从点A出发,沿折线AD-DO以每秒1个单位长度的速度向终点O运动,当点P与点A不重合时,过点P作PQ⊥AB于点Q,以PQ为边向右作正方形PQMN,设正方形PQMN与△ABD重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).
如图1,在矩形ABCD中,AB=4,BC=3,点O为对角线BD的中点,点P从点A出发,沿折线AD-DO以每秒1个单位长度的速度向终点O运动,当点P与点A不重合时,过点P作PQ⊥AB于点Q,以PQ为边向右作正方形PQMN,设正方形PQMN与△ABD重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com