

分析 (1)延长CD到H点,使DH=BF,连接AH,先证△ADH≌△ABF,再证△HAF≌△FAE即可解决问题.
(2)受(1)中证明的启示,先证出DE=EF+BF,由于CD=CB=6,则CE=BF+1,所示只需求出BF即可.BF在直角三角形ABF中,因此想办法用勾股定理解决问题,这样就需要先用BF表示出AF的平方,于是想到利用具有公共边的“子母型”相似来解决问题.AB是可求的,加上∠EAF=30°,故可延长BF至G,使∠AGF=30°,在FG上取点P构造∠PAF=30°,于是△AFP与△GFA子母型相似,柳暗花明又一村,自然有AF2=FP•FG,设BF为x,列出方程,解之即可,从而CE随之得解.值得一提的是,上述过程中,需证FP=FE,利用全等解决问题.
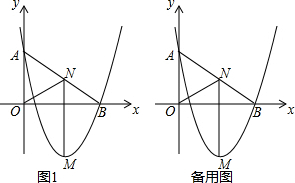
解答 解:(1)如图1,
延长CD到H点,使DH=BF,连接AH,
∵∠BAD=60°,∠BCD=120°,
∴∠D+∠B=180°,
∵∠ADE+∠ADH=180°,
∴∠ADH=∠B,
∵AD=AB,DH=BF,
∴在△ADH和△ABF中,
$\left\{\begin{array}{l}{DH=BF}\\{∠ADH=∠B}\\{AD=AB}\end{array}\right.$,
∴△ADH≌△ABF(SAS),
∴AH=AF,∠HAD=∠FAB,
∵∠DAB=60°,∠FAE=30°,
∴∠EAB+∠DAF=30°,
∴∠DAF+∠HAD=30°,即∠HAF=30°,
在△HAE和△EAF中,
$\left\{\begin{array}{l}{AH=AF}\\{∠HAE=∠EAF}\\{AE=AE}\end{array}\right.$,
∴△HAF≌△FAE(SAS),
∴HE=EF,
∵HE=HD+DE=BF+DE,
∴EF=DE+BF
(2)如图2,
连接AC,在DC上截取DN=BF,
∵AD=AB,CD=CB,AC=AC,
∴△ADC≌△ABC,
∴∠ADC=∠ABC,
∵∠DAB=60°,∠BCD=120°,
∴∠ADC=∠ABC=90°,∠CAD=∠CAB=30°,
∴△ADN≌△ABF,
∴AN=AF,∠FAB=∠DAN,
∵∠FAB+∠BAE=30°,
∴∠DAN+∠BAE=30°,
∴∠NAE=30°=∠FAE,
∴△ANE≌△AFE,
∴NE=EF,∠AEN=∠AEF,
作AM⊥EF于点M,则AM=AD=AB,
∴△AMF≌ABF,
∴∠MFA=∠BFA,
延长BF至G,使AGF=30°,在FG上取点P,使∠PAF=30°,
∵∠MFP=∠CFE,
∴∠AFP=∠AFE,
∴△AFP≌△AFE,且△AFP∽△GFA,
∴FP=FE=7,
∵CB=6,
∴AB=6$\sqrt{3}$,
∴BG=18,
设BF=x,
∵△AFP∽△GFA,
∴AF2=FP•FG=7(18-x)=126-7x,
∵AF2=AB2+BF2,
∴126-7x=108+x2,
解得:x=2,
即BF=2,
∵DE=CD+CE=EF+BF,
∴CE=3,
∴$\frac{BF}{CE}=\frac{2}{3}$.
点评 本题主要考查全等三角形的判定与性质,等腰三角形的性质,相似三角形的构造、相似三角形的判定与性质,截长补短技巧的应用,勾股定理等重要知识点和技能.正确地作出辅助线及严密的逻辑分析是关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图,在长方形纸片ABCD中,AB=mAD,其中m≥1,将它沿EF折叠(点E、F分在边AB、CD上),使点B落在AD边上的点M处,点C落在点N处,若∠BEF=α,$\frac{AM}{EF}$的值(用含m,α的式子表示).
如图,在长方形纸片ABCD中,AB=mAD,其中m≥1,将它沿EF折叠(点E、F分在边AB、CD上),使点B落在AD边上的点M处,点C落在点N处,若∠BEF=α,$\frac{AM}{EF}$的值(用含m,α的式子表示).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
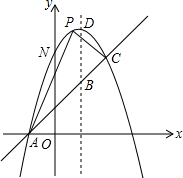 如图,已知抛物线y=-x2+bx+c过(1,4)与(4,-5)两点,且与一直线y=x+1相交于A,C两点,
如图,已知抛物线y=-x2+bx+c过(1,4)与(4,-5)两点,且与一直线y=x+1相交于A,C两点,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | -3 | C. | -2.5 | D. | -7.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com