Question

如图（1），A，E，F，C在一条直线上，AE=CF，过E，F分别作DE⊥AC，BF⊥AC，若AB=CD，试证明BD平分EF，若将△DEC的边EC沿AC方向移动变为图（2）时，其余条件不变，上述结论是否成立？请说明理由．

Answer 1

（1）先利用HL判定Rt△ABF≌Rt△CDE，得出BF=DE；再利用AAS判定△BFG≌△DGE，从而得出FG=EG，即BD平分EF．
（2）结论仍然成立，同样可以证明得到．

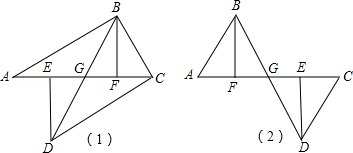
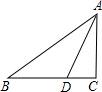
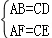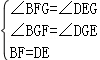试题分析：（1）先利用HL判定Rt△ABF≌Rt△CDE，得出BF=DE；再利用AAS判定△BFG≌△DGE，从而得出FG=EG，即BD平分EF．
（2）结论仍然成立，同样可以证明得到．
（1）证明：∵DE⊥AC，BF⊥AC，
∴∠DEG=∠BFE=90°．
∵AE=CF，AE+EF=CF+EF．
即AF=CE．
在Rt△ABF和Rt△CDE中，

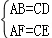
∴Rt△ABF≌Rt△CDE（HL），
∴BF=DE．
在△BFG和△DEG中，

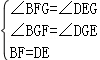
∴△BFG≌△DGE（AAS），
∴FG=EG，即BD平分EF．
（2）FG=EG，即BD平分EF的结论依然成立．
理由：因为 AE=CF，
所以 AF=CE，
因为 DE垂直于AC，BF垂直于AC，
所以 角AFB=角CED，BF∥DE，
因为 AB∥CD，
所以 角A=角C，
所以 三角形ABF全等于三角形CDE，
所以 BF=DE，
所以 四边形BEDF是平行四边形，
所以 GE=GF，即：BD平分EF，
即结论依然成立．
点评：本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．
注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．