
已知:如图等边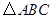 内接于⊙O,点
内接于⊙O,点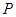 是劣弧
是劣弧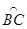 上的一点(端点除外),延长
上的一点(端点除外),延长 至
至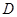 ,使
,使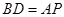 ,连结
,连结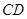 .
.
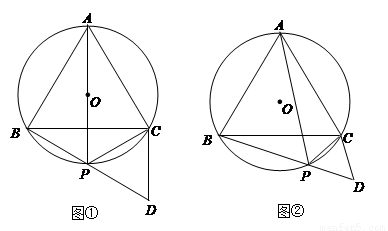
(1)若 过圆心
过圆心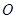 ,如图①,请你判断
,如图①,请你判断 是什么三角形?并说明理由.
是什么三角形?并说明理由.
(2)若 不过圆心
不过圆心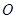 ,如图②,
,如图②, 又是什么三角形?为什么?
又是什么三角形?为什么?
(1)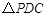 为等边三角形;(2)
为等边三角形;(2)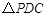 仍为等边三角形
仍为等边三角形
【解析】
试题分析:(1)根据等边三角形的性质可得AC=BC,根据圆周角定理可得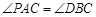 ,再结合
,再结合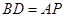 可证得
可证得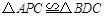 ,可得PC=DC,求得
,可得PC=DC,求得
即的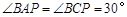 ,
,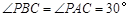 ,即可得到
,即可得到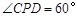 ,即得结果;
,即得结果;
(2)先证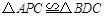 (过程同上)可得PC=DC,由
(过程同上)可得PC=DC,由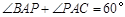 ,又
,又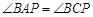 ,
,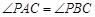 即可得到
即可得到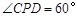 ,从而得到结果.
,从而得到结果.
(1)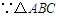 为等边三角形
为等边三角形
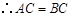 ,
,
又 在⊙O中
在⊙O中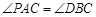
又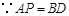
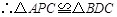 .
.
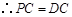
又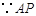 过圆心
过圆心 ,
,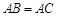 ,
,
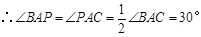
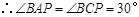 ,
,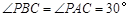
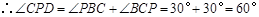
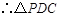 为等边三角形.
为等边三角形.
(2)先证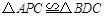 (过程同上)
(过程同上)
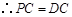

又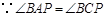 ,
,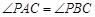

又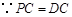
 为等边三角形.
为等边三角形.
考点:全等三角形的判定和性质,等边三角形的判定和性质
点评:全等三角形的判定和性质的应用是初中数学平面图形中极为重要的知识,贯穿于整个初中数学的学习,与各个知识点联系极为容易,因而是中考的热点,在各种题型中均有出现,一般难度不大,需特别注意.


科目:初中数学 来源: 题型:
| 3 |
 |
| AC |
 重合,连接AD并延长交BC的延长结于P.
重合,连接AD并延长交BC的延长结于P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 的等边三角形ABC内接于⊙O,点D在
的等边三角形ABC内接于⊙O,点D在 上运动,但与A、C两点不
上运动,但与A、C两点不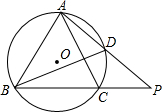 重合,连接AD并延长交BC的延长结于P.
重合,连接AD并延长交BC的延长结于P.查看答案和解析>>
科目:初中数学 来源:专项题 题型:解答题
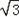 的等边三角形ABC内接于⊙O,点D在
的等边三角形ABC内接于⊙O,点D在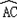 上运动,但与A、C两点不重合,连接AD并延长交BC的延长结于P.
上运动,但与A、C两点不重合,连接AD并延长交BC的延长结于P.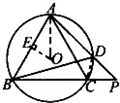
查看答案和解析>>
科目:初中数学 来源:2002年全国中考数学试题汇编《图形的相似》(04)(解析版) 题型:解答题
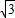 的等边三角形ABC内接于⊙O,点D在
的等边三角形ABC内接于⊙O,点D在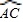 上运动,但与A、C两点不重合,连接AD并延长交BC的延长结于P.
上运动,但与A、C两点不重合,连接AD并延长交BC的延长结于P.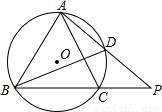
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com