
 ��ͼ����ƽ��ֱ������ϵ�У���֪����ABCD����������B��4��0����C��8��0����D��8��8����������y=ax2+bx��A��C���㣬����P�ӵ�A���������߶�AB���յ�B�˶���ͬʱ��Q�ӵ�C���������߶�CD���յ�D�˶����ٶȾ�Ϊÿ��1����λ���ȣ��˶�ʱ��Ϊt�룬����P��PE��AB��AC�ڵ�E��
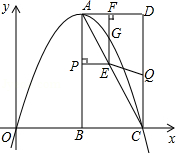
��ͼ����ƽ��ֱ������ϵ�У���֪����ABCD����������B��4��0����C��8��0����D��8��8����������y=ax2+bx��A��C���㣬����P�ӵ�A���������߶�AB���յ�B�˶���ͬʱ��Q�ӵ�C���������߶�CD���յ�D�˶����ٶȾ�Ϊÿ��1����λ���ȣ��˶�ʱ��Ϊt�룬����P��PE��AB��AC�ڵ�E������ ��1�������ı���ABCDΪ���Σ�����A����D����������ͬ��A����B���������ͬ��
��2���������������ε����ʣ��ɵ�PE��PB�ij����ɵ�E�����꣬����ƽ����y��ֱ���������ľ����ǽϴ�����������С�������꣬�ɵ�GE�ij������������ε������ʽ���ɵö��κ��������ݶ��κ��������ʣ��ɵô𰸣�
��3�������ɵ��������Σ���������������������ȼ��ɣ����ǿɷ�EQ=QC��EC=CQ��EQ=EC����������ۣ������������ʱ����ͬ�������߳�����ͬ��Ϊ���������Σ�
��� �⣺��1����Ϊ��B�ĺ�����Ϊ4����D��������Ϊ8��AD��x�ᣬAB��y�ᣬ���Ե�A������Ϊ��4��8����
��A��4��8����C��8��0����������ֱ����y=ax2+bx��$\left\{\begin{array}{l}{16a+4b=8}\\{64a+8b=0}\end{array}\right.$��
���$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=4}\end{array}\right.$��
�������ߵĽ���ʽΪ��y=-$\frac{1}{2}$x2+4x��
��2����PE��BC�����APE�ס�ABC��$\frac{PE}{BC}$=$\frac{AP}{AB}$����$\frac{PE}{4}$=$\frac{AP}{8}$��PE=$\frac{1}{2}$AP=$\frac{1}{2}$t��PB=8-t��
E��4+$\frac{1}{2}$t��8-t����G���������4+$\frac{1}{2}$t��-$\frac{1}{8}$t2+8����
GE=��-$\frac{1}{8}$t2+8��-��8-t��=-$\frac{1}{8}$t2+t��
S��AGC=$\frac{1}{2}$GE•��xC-xA��=$\frac{1}{2}$��-$\frac{1}{8}$t2+t����8-4��=-$\frac{1}{4}$��t-4��2+4��
��t=4ʱ����AGC�����������ֵΪ4��
��3���ٵ�EQ=QCʱ����Q��8��t����E��4+$\frac{1}{2}$t��8-t����QC=t��
���Ը����������빫ʽ���ã�
��$\frac{1}{2}$t-4��2+��8-2t��2=t2��
������13t2-144t+320=0��
���t=$\frac{40}{13}$��t=$\frac{104}{13}$=8����ʱE��C�غϣ����ܹ��������Σ���ȥ����
�ڵ�EC=CQʱ��
��ΪE��4+$\frac{1}{2}$t��8-t����C��8��0����QC=t��
���Ը����������빫ʽ���ã�
��4+$\frac{1}{2}$t-8��2+��8-t��2=t2��
������t2-80t+320=0��t=40-16$\sqrt{5}$��t=40+16$\sqrt{5}$��8����ʱQ���ھ��εı��ϣ���ȥ����
�۵�EQ=ECʱ��
��ΪQ��8��t����E��4+$\frac{1}{2}$t��8-t����C��8��0����
���Ը����������빫ʽ���ã���$\frac{1}{2}$t-4��2+��8-2t��2=��4+$\frac{1}{2}$t-8��2+��8-t��2��
���t=0����ʱQ��C�غϣ����ܹ��������Σ���ȥ����t=$\frac{16}{3}$��
����t1=$\frac{16}{3}$��t2=$\frac{40}{13}$��t3=40-16$\sqrt{5}$��
���� ���⿼���˶��κ����ۺ��⣬�����ߵ����Ǻ�������ʽ�е�һ�֣�ͨ��������ô���ϵ�����������з����飬����δ֪ϵ�������ַ�������Ƚ��ʺϣ�����ѹ�����еĶ������⡢��ֵ���⣬�ȸ����������Ծ��ƶ�������δ֪ϵ����ʾ���Ե����꣬����ܹ��ɶ��κ���������ͨ���䷽�����깫ʽ���伫ֵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4�� | B�� | 3�� | C�� | 2�� | D�� | 1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
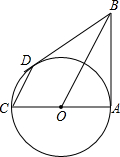 ��ͼ��AB���O�����ڵ�A��ACΪ��O��ֱ������AC=6��CD��BO��CD����O��D������BD��
��ͼ��AB���O�����ڵ�A��ACΪ��O��ֱ������AC=6��CD��BO��CD����O��D������BD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��3-��2=90�� | B�� | ��3+��2=90�� | C�� | ��3=��2 | D�� | û�й�ϵ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
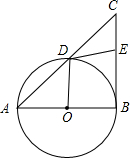 ��ͼ��Rt��ABC�У���ABC=90�㣬��ABΪֱ���ġ�O��AC�ڵ�D��EΪBC���е㣬����DE��OD��
��ͼ��Rt��ABC�У���ABC=90�㣬��ABΪֱ���ġ�O��AC�ڵ�D��EΪBC���е㣬����DE��OD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com