
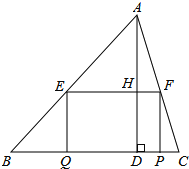
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,高
,高![]() , 矩形
, 矩形![]() 的一边
的一边![]() 在
在![]() 边上,
边上,![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,
上,![]() 交
交![]() 于点
于点![]() .
.
(1)求证:![]() ;
;
(2)设![]() ,当
,当![]() 为何值时,矩形
为何值时,矩形![]() 的面积最大?并求出最大面积;
的面积最大?并求出最大面积;
(3)当矩形![]() 的面积最大时,该矩形
的面积最大时,该矩形![]() 以每秒
以每秒![]() 个单位的速度沿射线
个单位的速度沿射线![]() 匀速向上运动(当矩形的边
匀速向上运动(当矩形的边![]() 到达
到达![]() 点时停止运动),设运动时间为
点时停止运动),设运动时间为![]() 秒,矩形
秒,矩形![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)当x为![]() 时,矩形的面积有最大值5;(3)S=
时,矩形的面积有最大值5;(3)S=
【解析】
(1)由条件可得EF∥BC,根据相似三角形的判定即可求证;
(2)由(1)可得![]() ,用x表示出HD,表示出矩形EFPQ的面积,利用二次函数可求得其最大值;
,用x表示出HD,表示出矩形EFPQ的面积,利用二次函数可求得其最大值;
(3)当0≤t<2时,设矩形EFPQ与AB、AC的交点分别为M、N、R、S,可利用平行表示出MN的长,可表示出△EMS和△NFR的面积,进一步可表示出重叠部分的面积;当2≤t≤4时,重叠部分为△P′Q′A,利用平行分别用x表示出其底和高,可表示出面积.
解:(1)∵四边形EFPQ为矩形,
∴EF∥BC,
∴![]() ;
;
(2)∵![]()
∴![]() ,即
,即![]() ,
,
∴HD=4-![]() ,
,
∴S矩形EFPQ=EFFQ=EFHD=x(4-![]() )=-
)=-![]() x2+4x,
x2+4x,
该函数为开口向下的二次函数,故当x=![]() 时有最大值,最大值为5,
时有最大值,最大值为5,
即当x为![]() 时,矩形的面积有最大值5;
时,矩形的面积有最大值5;
(3)由(2)可知,当矩形面积取最大值时,EF=![]() ,FQ=2,
,FQ=2,
①当0≤t≤2时,如图1,设矩形与AB、AC分别交与点M、N、R、S,与AD交于J、L,连接RS,交AD于K,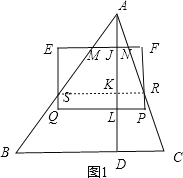
由题意可知LD=JK=t,则AJ=AD-LD-JL=4-t-2=2-t,
又∵RS=![]() ,
,
∴R、S为AB、AC的中点,
∴AK=![]() AD=2,ES=FR=JK=t,
AD=2,ES=FR=JK=t,
又∵MN∥RS,
∴![]() ,即
,即 ,
,
∴![]() -
-![]() t,
t,
∴EM+FN=EF-MN=![]() -(
-(![]() -
-![]() t)=
t)=![]() t,
t,
∴S△EMS+S△FNR=![]() ES(EM+FN)=
ES(EM+FN)=![]() t
t![]() t=
t=![]() ,
,
∴S=S矩形EFPQ-(S△EMS+S△FNR)=5-![]() ;
;
②当2<t≤4时,如图2,设矩形与AB、AC、AD分别交于点Q′、P′、D′,
根据题意D′D=t,则AD′=4-t,
∵PQ∥BC,
∴![]() ,即
,即![]() ,
,
解得P′Q′=5-![]() t,
t,
∴S=S△AP′Q′=![]() P′Q′AD′=
P′Q′AD′=![]() (4-t)(5-
(4-t)(5-![]() t)=
t)=![]() -5t+10;
-5t+10;
综上可知S= .
.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】已知如图所示,在Rt△ABC中,∠A=90°,∠BCA=75°,AC=8cm,DE垂直平分BC,则BE的长是( )
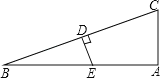
A.4cmB.8cmC.16cmD.32cm
查看答案和解析>>
科目:初中数学 来源: 题型:
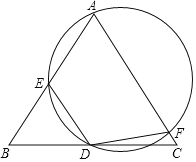
【题目】如图,在△ABC中,AB=AC,点D为BC的中点,经过AD两点的圆分别与AB,AC交于点E、F,连接DE,DF.
(1)求证:DE=DF;
(2)求证:以线段BE+CF,BD,DC为边围成的三角形与△ABC相似,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=﹣x2+bx+c的对称轴为直线x=2,且顶点在x轴上.
(1)求b、c的值;
(2)画出抛物线的简图并写出它与y轴的交点C的坐标;
(3)根据图象直接写出:点C关于直线x=2对称点D的坐标 ;若E(m,n)为抛物线上一点,则点E关于直线x=2对称点的坐标为 (用含m、n的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,分别沿长方形纸片ABCD和正方形纸片EFGH的对角线AC,EG剪开,拼成如图2所示的ALMN,若中间空白部分四边形OPQR恰好是正方形,且ALMN的面积为50,则正方形EFGH的面积为( )
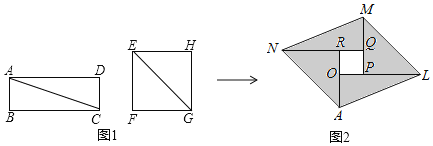
A. 24 B. 25 C. 26 D. 27
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实“垃圾分类”,环卫部门要求垃圾要按A,B,C三类分别装袋,投放,其中A类指废电池,过期药品等有毒垃圾,B类指剩余食品等厨余垃圾,C类指塑料,废纸等可回收垃圾.甲投放了一袋垃圾,乙投放了两袋垃圾,这两袋垃圾不同类.
(1)直接写出甲投放的垃圾恰好是A类的概率;
(2)求乙投放的垃圾恰有一袋与甲投放的垃圾是同类的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
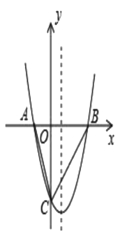
【题目】如图,在平面直角坐标系中,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() .
.
(1)求抛物线的解析式;
(2)点![]() 在抛物线的对称轴上,当
在抛物线的对称轴上,当![]() 的周长最小时,点
的周长最小时,点![]() 的坐标为_____________;
的坐标为_____________;
(3)点![]() 是第四象限内抛物线上的动点,连接
是第四象限内抛物线上的动点,连接![]() 和
和![]() .求
.求![]() 面积的最大值及此时点
面积的最大值及此时点![]() 的坐标;
的坐标;
(4)若点![]() 是对称轴上的动点,在抛物线上是否存在点
是对称轴上的动点,在抛物线上是否存在点![]() ,使以点
,使以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形?若存在,请直接写出点
为顶点的四边形是平行四边形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() 是
是![]() 的角平分线,
的角平分线,![]() ,
,![]() 在
在![]() 边上,以
边上,以![]() 为直径的半圆
为直径的半圆![]() 经过点
经过点![]() ,交
,交![]() 于点
于点![]() .
.

(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)已知![]() ,
,![]() 的半径为
的半径为![]() ,求图中阴影部分的面积.(最后结果保留根号和
,求图中阴影部分的面积.(最后结果保留根号和![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=4,BC=3.
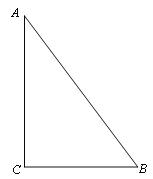
(1)该三角形的外接圆的半径长等于 ;
(2)用直尺和圆规作出该三角形的内切圆(不写作法,保留作图痕迹),并求出该三角形内切圆的半径长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com