
分析 根据锐角三角函数关系式,得sin2A+sin2B=1;根据一元二次方程根与系数的关系,得sinA+sinB=$\sqrt{2}$,sinA•sinB=-k,再进一步利用完全平方公式得到关于k的方程进行求解.
解答 解:∵sinA和sinB是方程x2-$\sqrt{2}$x-k=0的两个根,
∴sinA+sinB=$\sqrt{2}$,sinA•sinB=-k,
∵Rt△ABC中,∠C=90°,
∴sin2A+sin2B=1,
∴2+2k=1,
解得,k=-$\frac{1}{2}$.
∵sinA+sinB=$\sqrt{2}$,sinA•sinB=$\frac{1}{2}$,
∴sinA=sinB=$\frac{\sqrt{2}}{2}$,
∴∠A=∠B=45°.
故答案为45°,45°,-$\frac{1}{2}$.
点评 此题综合考查了一元二次方程根与系数的关系:x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.也考查了锐角三角函数关系式.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在Rt△ABC中,∠C=90°,将其绕B点顺时针旋转一周,则分别以BA,BC为半径的圆形形成一圆环(阴影部分),为求该圆环的面积,只需测量一条线段的长度,这条线段就是( )
如图,在Rt△ABC中,∠C=90°,将其绕B点顺时针旋转一周,则分别以BA,BC为半径的圆形形成一圆环(阴影部分),为求该圆环的面积,只需测量一条线段的长度,这条线段就是( )| A. | AD | B. | AB | C. | BD | D. | AC |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 运算程序 | 例如 | 按左侧的形式完成你的举例 |
| ①给出任意一个三位数 | 325 | 123 |
| ②重复①中的数,得到一个新的数字 | 325325 | 123123 |
| ③将②的结果除以7 | 325325÷7=a46475 | 123123÷7=17589 |
| ④将③的结果除以11 | a÷11=b4225 | 17589÷11=1599 |
| ⑤将④的结果除以13 | b÷13=325 | 1599÷13=123 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
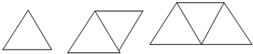 请你拿出火柴棒,现在我们来用火柴棒搭如图所示的三角形.
请你拿出火柴棒,现在我们来用火柴棒搭如图所示的三角形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com