
【题目】9月、10月是房地产行业的传统销售旺季,素来有“金九银十”之称,重庆某开发商两江新区项目部为了赶上销售旺季,在今年9月推出小高层和洋房两种房型共100套,其中洋房每价格是小高层每套价格的2倍.
(1)该项目部9月份推出的两种房型全部售完,其中小高层销售额为7200万元,洋房销售额为9600万元,则小高层每套价格为多少万元?
(2)国家明确表态:“坚持房子是用来住的,不是用来炒的,落实房地产长效管理机制,不将房地产作为短期刺激经济的手段.”随后出台“银行资金不得流向房市”等相关政策.受政策及经济大环境影响,市民购房欲望下降,房市遇冷,在(1)问的基础上,10月份小高层每套降价a%,洋房每套降价2a%:为完成10月份销售任务,该项目部决定小高层的套数增加![]() a%,洋房的套数增加
a%,洋房的套数增加![]() %;到月底,小高层卖出95%,洋房卖出80%;为回笼资金,该项目部在该月最后一天推出6套“钜惠”商铺,每套380万元,且成功将6套商铺全部售出,最终实现10月份总销售额在9月份总销售额基础上增加
%;到月底,小高层卖出95%,洋房卖出80%;为回笼资金,该项目部在该月最后一天推出6套“钜惠”商铺,每套380万元,且成功将6套商铺全部售出,最终实现10月份总销售额在9月份总销售额基础上增加![]() a%,求a的值.
a%,求a的值.
【答案】(1)小高层每套价格为120万元;(2)a的值为5.
【解析】
(1)设小高层每套价格为x万元,今年9月份推出y套小高层,则洋房每套的价格为2x万元,推出(100y)套洋房,根据总价=单价×数量,即可得出关于x,y的方程组,解之即可得出结论;
(2)根据总价=单价×数量,即可得出关于a的一元二次方程,利用换元法解一元二次方程后,即可得出结论.
(1)设小高层每套价格为x万元,今年9月份推出y套小高层,则洋房每套的价格为2x万元,推出(100﹣y)套洋房,
依题意,得:![]() ,
,
解得:![]() .
.
答:小高层每套价格为120万元.
(2)依题意,得:120(1﹣a%)×60(1+![]() a%)×95%+120×2(1﹣2a%)×(100﹣60)(1+
a%)×95%+120×2(1﹣2a%)×(100﹣60)(1+![]() %)×80%+380×6=(7200+9600)(1+
%)×80%+380×6=(7200+9600)(1+![]() a%),
a%),
令m=a%,则原方程可整理得:20m2﹣m=0,
解得:m1=0(舍去),m2=![]() .
.
∵m=a%,即![]() =a%,
=a%,
∴a=5.
答:a的值为5.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确的是( )

A. ①②④ B. ①②⑤ C. ②③④ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC分别交AC的延长线于点E,交AB的延长线于点F.
(1)求证:EF是⊙O的切线;
(2)若AC=8,CE=4,求弧BD的长.(结果保留π)
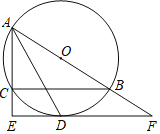
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国庆期间,《我和我的祖国》、《中国机长》、《攀登者》这三部电影在全国各大影院热映,某影院有A、B、C三类观影厅,可容纳的观影人数分别为100人,60人,80人.三部电影在各播放厅的票价如下:
A类厅 | B类厅 | C类厅 | |
《我和我的祖国》 | 30元 | 36元 | 无 |
《中国机长》 | 40元 | 45元 | 50元 |
《攀登者》 | 40元 | 45元 | 无 |
10月6日那天,在A类厅,《我和我的祖国》的播放场次是《攀登者》的播放场次的1.5倍,《中国机长》的播放场次比《我和我的祖国》的播放场次多3场;在B类厅,《攀登者》的播放场次是《我和我的祖国》的播放场次的一半,《中国机长》的播放场次比《我和我的祖园》的播放场次的![]() 多1场;《中国机长》在C类厅的播放场次比在A类厅的播放场次的
多1场;《中国机长》在C类厅的播放场次比在A类厅的播放场次的![]() 多1场:《攀登者》在B类厅的播放场次是在A类厅播放场次的
多1场:《攀登者》在B类厅的播放场次是在A类厅播放场次的![]() 倍;B类厅当天的总播放场次不超过50场.已知《我和我的祖国》和《中国机长》在各类厅的平均售票率为80%,在各种票都以原价售出的前提下,当《攀登者》的售票率至少为_____时,才能保证该影院当天这三部电影的销售额不低于200520元.
倍;B类厅当天的总播放场次不超过50场.已知《我和我的祖国》和《中国机长》在各类厅的平均售票率为80%,在各种票都以原价售出的前提下,当《攀登者》的售票率至少为_____时,才能保证该影院当天这三部电影的销售额不低于200520元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形 ABCD 的对角线 AC 与 BD 相交于点 O,CE∥BD, DE∥AC , AD=2![]() , DE=2,则四边形 OCED 的面积为( )
, DE=2,则四边形 OCED 的面积为( )

A. 2![]() B. 4 C. 4
B. 4 C. 4![]() D. 8
D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+(2m﹣1)x﹣2m(m>0.5)的最低点的纵坐标为﹣4.
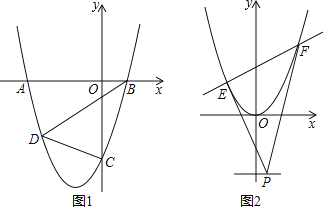
(1)求抛物线的解析式;
(2)如图1,抛物线与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,D为抛物线上的一点,BD平分四边形ABCD的面积,求点D的坐标;
(3)如图2,平移抛物线y=x2+(2m﹣1)x﹣2m,使其顶点为坐标原点,直线y=﹣2上有一动点P,过点P作两条直线,分别与抛物线有唯一的公共点E、F(直线PE、PF不与y轴平行),求证:直线EF恒过某一定点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的BC边上一点O为圆心的圆,经过A、B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,若AC=FC.
(1)求证:AC是⊙O的切线:
(2)若BF=8,DF=![]() ,求⊙O的半径;
,求⊙O的半径;
(3)若∠ADB=60°,BD=1,求阴影部分的面积.(结果保留根号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com