
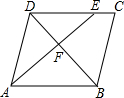
 如图所示,在?ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为9:16.
如图所示,在?ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为9:16. 科目:初中数学 来源: 题型:选择题
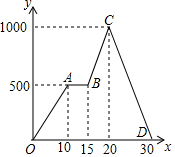 宇嘉同学从家出发沿笔直的公路去晨练,他离开家的距离y(米)与时间x(分)的函数关系图象如图所示.下列结论中,不正确的是( )
宇嘉同学从家出发沿笔直的公路去晨练,他离开家的距离y(米)与时间x(分)的函数关系图象如图所示.下列结论中,不正确的是( )| A. | 整个行进过程花了30分钟 | B. | 整个行进过程共走了1000米 | ||
| C. | 在图中停下来休息了5分钟 | D. | 返回时速度为100米/分 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,为了测量矗立在高速公路水平地面上的交通警示牌的高度CD,在距M相距4米的A处,测得警示牌下端D的仰角为45°,再笔直往前走8米到达B处,在B处测得警示牌上端C的仰角为30°,求警示牌的高度CD.(结果精确到0.1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
如图,为了测量矗立在高速公路水平地面上的交通警示牌的高度CD,在距M相距4米的A处,测得警示牌下端D的仰角为45°,再笔直往前走8米到达B处,在B处测得警示牌上端C的仰角为30°,求警示牌的高度CD.(结果精确到0.1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
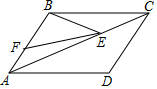 已知,如图,在?ABCD中,BE、CE分别平分∠ABC、∠BCD,E为AD上,BE=12cm,CE=5cm,则?ABCD的周长为39cm.
已知,如图,在?ABCD中,BE、CE分别平分∠ABC、∠BCD,E为AD上,BE=12cm,CE=5cm,则?ABCD的周长为39cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
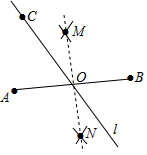 数学课上,老师提出如下问题:已知点A,B,C是不在同一直线上三点,求作一条过点C的直线l,使得点A,B到直线l的距离相等.
数学课上,老师提出如下问题:已知点A,B,C是不在同一直线上三点,求作一条过点C的直线l,使得点A,B到直线l的距离相等.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com