
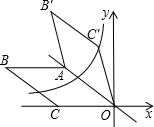
 如图所示,在平面直角坐标系中,菱形OABC的顶点A的坐标是(-4,3),顶点C的坐标为(-5,0),将菱形OABC沿边OA所在直线翻折,得到菱形OAB′C′,若反比例函数y=$\frac{k}{x}$(x<0)的图象刚好经过点C′,则k的值为$-\frac{168}{25}$.
如图所示,在平面直角坐标系中,菱形OABC的顶点A的坐标是(-4,3),顶点C的坐标为(-5,0),将菱形OABC沿边OA所在直线翻折,得到菱形OAB′C′,若反比例函数y=$\frac{k}{x}$(x<0)的图象刚好经过点C′,则k的值为$-\frac{168}{25}$. 分析 连接CC′,过点C′作C′E⊥OC,垂足为E.由点A的坐标可知:tan∠AOC=$\frac{3}{4}$,由锐角三角函数的定义可知求得CD=3,从而可得到CC′=6,然后在Rt△C′CE中依据锐角三角函数的定义可求得CE、C′E的长度,从而可求得点C′的坐标,于是可求得k的值.
解答 解:连接CC′,过点C′作C′E⊥OC,垂足为E.
∵点A的坐标为(-4,3)
∴tan∠AOC=$\frac{3}{4}$.
∴tan∠DCO=$\frac{4}{3}$.
由翻折的性质可知:CC′⊥AO,CD=C′D.
∴CD=OCsin∠COD=$5×\frac{3}{5}$=3.
∴CC′=6.
∴CE=CC′cos∠C′CE=6×$\frac{3}{5}$=$\frac{18}{5}$,C′E=CC′sin∠C′CE=6×$\frac{4}{5}$=$\frac{24}{5}$.
∴EO=OC-CE=5-$\frac{18}{5}$=$\frac{7}{5}$.
∴点C′的坐标为(-$\frac{7}{5}$,$\frac{24}{5}$).
k=$-\frac{7}{5}$×$\frac{24}{5}$=-$\frac{168}{25}$.
故答案为:-$\frac{168}{25}$.
点评 本题主要考查的是翻折的性质,锐角三角函数的定义,反比例函数,利用翻折的性质和锐角三角函数的定义求得点C′的坐标是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com