Question

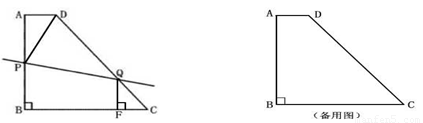
如图，已知直角梯形ABCD中，AD∥BC，AB⊥BC ，AD＝2cm，AB＝8cm，CD＝10cm．

(1)求梯形ABCD的周长；

(2)动点P从点B出发，以1cm/s的速度沿B→A→D→C方向向点C运动；动点Q从点C出发，以1cm/s的速度沿C→D→A方向向点A运动；过点Q作QF⊥BC于点F．若P、Q两点同时出发，当其中一点到达终点时整个运动随之结束，设运动时间为t秒．问：

在运动过程中，是否存在这样的t，使得以P、D、Q为顶点的三角形恰好是以DQ为一腰的等腰三角形？若存在，请求出所有符合条件的t的值；若不存在，请说明理由．

 

Answer 1

【答案】

(1) 28cm(2) 当t=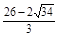或8≤t＜10或10＜t≤12时，以P、D、Q为顶点的三角形恰好是以DQ为一腰的等腰三角形

【解析】解：（1）过点D作DE⊥BC于点E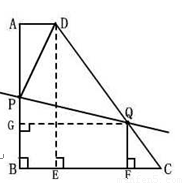

       ∵四边形ABCD是直角梯形

       ∴四边形ABED是矩形

       ∴AD=BE=2，AB=DE=8

       在Rt△DEC中，CE=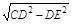==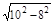6

      ∴梯形ABCD的周长= AB+BC+CD+DA=8+8+10+2=28cm.

………3分

（2） ① 当0≤t≤8时，过点Q作QG⊥AB于点G

      则AP=8－t，DQ=10－t，AD=2，

      ∵Rt△CQF∽Rt△CDE

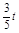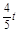∴CF=，QF=，∴PG=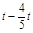=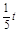，QG=8－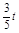

=（8－t）²+2²=t²－16t+68，

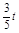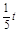PQ²=QG²+PG²=（8－）²+（）²=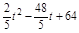 

若DQ=PD，则（10－t）²= t²－16t+68，解得：t=8；…………………5分

若DQ=PQ，则（10－t）²=，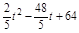       

解得：t₁=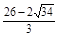 ，t₂=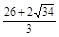＞8（舍去），此时t=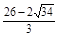；………6分

②当8＜t＜10时，PD=DQ=10－t，                

      ∴此时以DQ为一腰的等腰△DPQ恒成立； ……………………7分

③当t=10时，点P、D、Q三点重合，无法构成三角形；………………………8分

④当10＜t≤12时，PD=DQ= t－10，

      ∴此时以DQ为一腰的等腰△DPQ恒成立；      ………………………9分

综上所述，当t=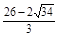或8≤t＜10或10＜t≤12时，以P、D、Q为顶点的三角形恰好是以DQ为一腰的等腰三角形.                 ………………………10分

（1）过点D作DE⊥BC于点E，然后求出AD=BE=2，AB=DE=8，在Rt△DEC中，根据CE= 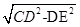求出CE，即可求出BC的长，从而求得梯形ABCD的周长

（2）（i）当0≤t≤8时，过点Q作QG⊥AB于点G，过点Q作QF⊥CB于点F，根据△CQF∽△CDE得出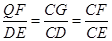，所以C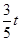F= ，QF= 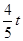，所以PG=t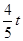= 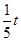，QG=8-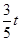，然后分别用t表示出PD²=t²-16t+68，PQ²=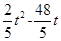+64，若DQ=PD，则（10-t）²=t²-16t+68，若DQ=PQ，则（10-t）²=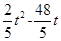+64，最后解方程即可；

（ii）当8＜t＜10时，PD=DQ=10-t，此时以DQ为一腰的等腰△DPQ恒成立；而当t=10时，点P、D、Q三点重合，无法构成三角形，当10＜t≤12时，PD=DQ= t－10，此时以DQ为一腰的等腰△DPQ恒成立，从而得出最后答案；