在平面直角坐标系中，有反比例函数y =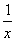 
与y = 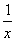－ 的图象和正方形ABCD，原点O 与对角线AC、BD的交点重叠，且如图所示的阴影部分面积为8，则AB= ．
科目：初中数学 来源： 题型：
已知正比例函数y=kx与反比例函数y=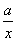
相交于点A(1,b)、点B(c,-2)，求k+a的值。甲同学说：未知数太多，很难求的；乙同学说：可能不是用待定系数法来求；丙说：如果用数形结合的方法，利用两交点在坐标系中位置的特殊性，可以试试。请结合他们的讨论求出k+a=________．
查看答案和解析>>
科目：初中数学 来源： 题型：
直角坐标系xoy中，一次函数y=kx+b（kb≠0）的图象过点（1，kb），且b≥2，与x轴、y轴分别交于A、B两点．设△ABO的面积为S，则S的最小值是（ ）
A．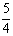
B．1 C．
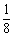D． 不存在
查看答案和解析>>
科目：初中数学 来源： 题型：
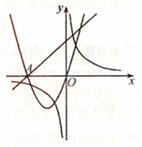
一次函数y=ax+b(a≠0)、二次函数y=ax2+bx和反比例函数y=k/x在同一直角坐标系中的图像如图所示，A点的坐标为（－2，0），则下列结论中，正确的是 （ ）
A．b=2a+k B．a=b+k C．a>b>0 D．a>k>0
查看答案和解析>>
科目：初中数学 来源： 题型：
在一个不透明的盒子中放有三张卡片，每张卡片上写有一个实数，分别为2，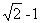
，
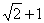，1。（卡片除了实数不同外，其余均相同）
（1）从盒子中随机抽取一张卡片，请直接写出卡片上的实数是有理数的概率；
（2）先从盒子中随机抽取两张卡片，将卡片上的实数相乘，请你用列表法或树状图（树形图）法，求出抽取的卡片上的实数之积为整数的概率。
查看答案和解析>>
科目：初中数学 来源： 题型：
设边长为3的正方形的对角线长为a，下列关于a的四种说法： a是无理数；‚ a可以在数轴上用一个点来表示；ƒ 3<a<4； „ a是18的算术平方根。其中，所有正确说法的序号是
A. „ B. ‚ƒ C. ‚„ D. ƒ„
查看答案和解析>>
科目：初中数学 来源： 题型：
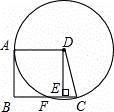
如图，在梯形ABCD中，AD∥BC，DA=DC，以点D为圆心，DA长为半径的⊙D与AB相切于A，与BC交于点F，过点D作DE⊥BC，垂足为E．
（1）求证：四边形ABED为矩形；
（2）若AB=4，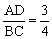
，求CF的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，正方形
的顶点
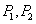在反比例函数
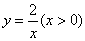的图像上，顶点
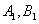分别在
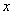轴，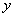
轴的正半轴上，再在其右侧作正方形
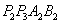，顶点
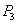在反比例函数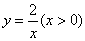的图像上，顶点
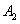在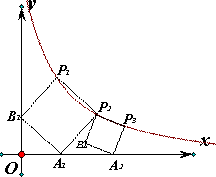
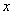轴的正半轴上，则点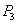的坐标为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
