
【题目】如图,在![]() 中,
中, ![]() ,点
,点![]() 为边
为边![]() 上一点,
上一点, ![]() ,且
,且![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,连接
,连接![]() ,又
,又![]() 的
的![]() 边上的高为
边上的高为![]() .
.
(1)判断直线![]() 是否平行?并说明理由;
是否平行?并说明理由;
(2)证明: ![]() .
.

【答案】(1) ![]() ,理由见解析;(2)见解析
,理由见解析;(2)见解析
【解析】试题分析:(1)先根据轴对称的性质得出PC=PD,AD=AC,∠APC=∠APD,再根据三角形外角的性质求出∠APC=60°,进而求出∠BPD=60°,由条件可得BP=![]() PD,取DP的中点E,易证△BPE为等边三角形,根据等边三角形的性质和三角形外角的性质求出∠DBE=30°,进而求出∠DBP=90°,根据平行线的判定即可得出结论;
PD,取DP的中点E,易证△BPE为等边三角形,根据等边三角形的性质和三角形外角的性质求出∠DBE=30°,进而求出∠DBP=90°,根据平行线的判定即可得出结论;
(2)作ΔADP的PD边上的高为AF,又作AG⊥BD交BD的延长线于G,根据对称性得出AF=AH,再求得∠GBA=45°,证明△AGB≌△AHB,得出AG=AH=AF,根据角平分线的判定得出AD平分∠GDP,进而求得∠GDA=75°,再根据对称性求得∠CAH=∠DAF=∠GAD=15°,从而得出结论.
试题解析:
解:(1)BD//AH.
证明:∵点C关于直线PA的对称点为D,
∴PC=PD,AD=AC,∠APC=∠APD.
又∵ ∠ABC=45°,∠PAB=15°,
∴∠APC=∠ABC+∠PAB=60°,
∴∠DPB=180°-∠DPA-∠APC=60°.
∵BC=3BP,∴BP=![]() PC,
PC,
∴BP=![]() PD;
PD;
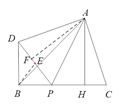
取PD的中点E,连接BE,则PE=PB,
∴△BPE为等边三角形,
∴BE=PE=DE,
∴∠DBE=∠BDE=![]() ∠BEP=30°.
∠BEP=30°.
∴∠DBP=∠DBE+∠EBP=90°.
又∵ AH⊥PC,∴∠AHC=90°,
∴∠DBP=∠AHC,∴DB//AH;
(2)证明:作ΔADP的PD边上的高为AF,又作AG⊥BD交BD的延长线于G,
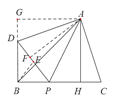
由对称性知,AF=AH.
∵∠GBA=∠GBC-∠ABC=45°,
∴∠GBA=∠HBA=45°,
∴AG=AH,
∴AG=AF,
∴AD平分∠GDP,
∴∠GDA=![]() ∠GDP=
∠GDP=![]() (180°-∠BDP) =75°.
(180°-∠BDP) =75°.
∴∠CAH=∠DAF=∠GAD=90°-∠GDA=15°,
∵∠BAP=15°,
∴∠BAP=∠CAH.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:
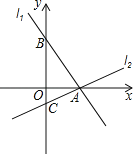
【题目】如图,过点A(2,0)的两条直线l1,l2分别交y轴于点B,C,其中点B在原点上方,点C在原点下方,已知AB=![]() .
.
(1)求点B的坐标;
(2)若△ABC的面积为4,求直线l2的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
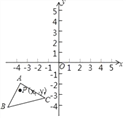
【题目】如图,△A′B′C′是△ABC经过平移得到的,△ABC三个顶点的坐标分别为A(﹣4,﹣1),B(﹣5,﹣4),C(﹣1,﹣3),△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4)
(1)请写出三角形ABC平移的过程;
(2)写出点A′,C′的坐标;
(3)求△A′B′C′的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AM∥CN,点B为平面内一点,AB⊥BC于B.
(1)如图1,直接写出∠A和∠C之间的数量关系________;
(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C;
(3)如图3,在(2)问的条件下,点E、F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,求∠EBC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知2辆A型车和1辆B型车载满货物一次可运货10吨.用1辆A型车和2辆B型车载满货物一次可运货11吨.某物流公司现有31吨货物,计划同时租用A型车a辆和B型车b辆,一次运完,且每辆车都满载货物.根据以上信息解答下列问题:
(1)1辆A型车和1辆B型车载满货物一次分别可运货物多少吨?
(2)请帮助物流公司设计租车方案
(3)若A型车每辆车租金每次100元,B型车每辆车租金每次120元.请选出最省钱的租车方案,并求出最少的租车费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P(x,y),若点Q的坐标为(x+ay,ax+y)(其中a为常数,且a≠0),则称Q是点P的“a系联动点”.例如:点P(1,2)的“3系联动点”Q的坐标为(7,5).
(1)点(3,0)的“2系联动点”的坐标为 ;若点P的“![]() 系联动点”的坐标是(
系联动点”的坐标是(![]() ,0),则点P的坐标为 ;
,0),则点P的坐标为 ;
(2)若点P(x,y)的“a系联动点”与“![]() 系联动点”均关于x轴对称,则点P分布在 ,请证明这个结论;
系联动点”均关于x轴对称,则点P分布在 ,请证明这个结论;
(3)在(2)的条件下,点P不与原点重合,点P的“a系联动点”为点Q,且PQ的长度为OP长度的3倍,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com