
【题目】以四边形ABCD的边AB、AD为底边分别作等腰三角形ABF和ADE.
(1)当四边形ABCD为正方形时(如图①),以边AB、AD为斜边分别向外侧作等腰直角三角形ABF和ADE,连接EB、FD,线段BE与DF的数量关系是:![]() = ;
= ;
(2)当四边形ABCD为矩形时(如图②),以边AB、AD为斜边分别向矩形内侧、外侧作等腰直角三角形ABF和ADE,连接EF、BD,线段EF与BD的数量关系是:![]() = ,请填空并说明理由;
= ,请填空并说明理由;
(3)当四边形ABCD为平行四边形时,以边AB、AD为底边分别向平行四边形内侧、外侧作等腰三角形ABF和ADE,且△EAD与△FBA的顶角∠AED=∠AFB=![]() ,连接EF、BD,交点为G.请用
,连接EF、BD,交点为G.请用![]() 表示出∠EGD,并说明理由.
表示出∠EGD,并说明理由.

【答案】(1)1;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据△ABF和△ ADE是等腰直角三角形,四边形ABCD是正方形,
求得△EBF≌△DEF,得到BE=DF;
(2)根据△ABF和△ ADE是等腰直角三角形,四边形ABCD是长方形,
求得△EAF~△DAB,得到![]() ;
;
(3)根据等腰三角形ABF和ADE的顶角∠AED=∠AFB=![]() ,∠EAD=∠EDA=∠FAB=∠FBA=
,∠EAD=∠EDA=∠FAB=∠FBA=![]() ,所以△EAD~△FAB,再求得△EAF~△DAB和△PAE~△PGD,最后求得∠EGD=∠EAD=
,所以△EAD~△FAB,再求得△EAF~△DAB和△PAE~△PGD,最后求得∠EGD=∠EAD=![]() .
.
(1)1;…………………………………………3’
(2)![]() ;…………………………………………4’
;…………………………………………4’
证明:∵△ABF和△ADE是等腰直角三角形
∴![]() ,∠EAD=45°,∠BAF=45°,…………………………………………5’
,∠EAD=45°,∠BAF=45°,…………………………………………5’
∵四边形ABCD是矩形
∴∠BAD=900,
∴∠FAD=∠BAD-∠BAF=45°,
∴∠EAF=∠FAD+∠EAD=90°,
∴∠EAF=∠BAD=90°…………………………………………6’
∴△EAF~△DAB…………………………………………7’
∴![]() …………………………………………8’
…………………………………………8’
(3)设EF与AD的交点为P点
∵等腰三角形ABF和ADE的顶角∠AED=∠AFB=![]()
∴∠EAD=∠EDA=∠FAB=∠FBA=![]()
∴△EAD~△FAB…………………………………………9’
∴![]()
∴![]()
∵∠EAD+∠DAF=∠FAB+∠DAF
即:∠EAF=∠DAB
∴△EAF~△DAB…………………………………………10’
∴∠AEF=∠ADB
又∵∠APE=∠GPD
∴△PAE~△PGD…………………………………………11’
∴∠EGD=∠EAD=![]() …………………………………………12’
…………………………………………12’


 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
【题目】如图,对称轴为直线x=![]() 的抛物线经过点A(6,0)和B(0,4).
的抛物线经过点A(6,0)和B(0,4).
(1)求抛物线解析式及顶点坐标;
(2)设点E(x,y)是抛物线上一动点,且位于第四象限,四边形OEAF是以OA为对角线的平行四边形,求四边形OEAF的面积S与x之间的函数关系式,并写出自变量x的取值范围;
(3)①当四边形OEAF的面积为24时,请判断OEAF是否为菱形?
②是否存在点E,使四边形OEAF为正方形?若存在,求出点E的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
(1)该玩具销售单价定为多少元时,商场能获得12000元的销售利润?
(2)该玩具销售单价定为多少元时,商场获得的销售利润最大?最大利润是多少?
(3)若玩具厂规定该品牌玩具销售单价不低于46元,且商场要完成不少于500件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() .
.

(1)尺规作图(保留作图痕迹,不写作法与证明):
①作![]() 的平分线
的平分线![]() 交边
交边![]() 于点
于点![]() ;
;
②过点![]() 作
作![]() 于点
于点![]() ;
;
(2)在(1)所画图中,若![]() ,
,![]() ,则
,则![]() 长为________________.
长为________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,AD是BC边上的中线.求证:AD⊥BC.
(填空)

证明:∵AD是BC边上的中线
∴BD=CD(中线的意义)
在△ABD和△ACD中
∵ 
①________;②________;③________.
∴ ________≌ ________(________)
∴∠ADB=________(________)
∴∠ADB= ![]() ∠BDC=90°(平角的定义)
∠BDC=90°(平角的定义)
∴AD⊥BC(垂直的定义)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了传承中华优秀传统文化,市教育局决定开展“经典诵读进校园”活动,某校团委组织八年级100名学生进行“经典诵读”选拔赛,赛后对全体参赛学生的成绩进行整理,得到下列不完整的统计图表。
组别 | 分数段 | 频次 | 频率 |
A | 60x<70 | 17 | 0.17 |
B | 70x<80 | 30 | a |
C | 80x<90 | b | 0.45 |
D | 90x<100 | 8 | 0.08 |
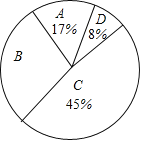
请根据所给信息,解答以下问题:
(1)表中a=___,b=___;
(2)请计算扇形统计图中B组对应扇形的圆心角的度数;
(3)已知有四名同学均取得98分的最好成绩,其中包括来自同一班级的甲、乙两名同学,学校将从这四名同学中随机选出两名参加市级比赛,请用列表法或画树状图法求甲、乙两名同学都被选中的概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF=![]() ∠CAB.
∠CAB.
(1)求证:直线BF是⊙O的切线;
(2)若AB=5,sin∠CBF=![]() ,求BC和BF的长.
,求BC和BF的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com