分析:探究:(1)根据水面与水平面平行可以得到CQ与BE平行,利用勾股定理即可求得BD的长:

。
(2)液体正好是一个以△BCQ是底面的直棱柱,据此即可求得液体的体积;。
(3)根据液体体积不变,据此即可列方程求解。
拓展:分容器向左旋转和容器向右旋转两种情况讨论。
延伸:当α=60°时,如图6所示,设FN∥EB,GB′∥EB,过点G作GH⊥BB′于点H,此时容器内液体形成两层液面,液体的形状分别是以Rt△NFM和直角梯形MBB′G为底面的直棱柱,求得棱柱的体积,即可求得溢出的水的体积,据此即可作出判断。
探究:(1)CQ∥BE, 3。
(2)

。
(3)在Rt△BCQ中,

,∴α=∠BCQ=37°。
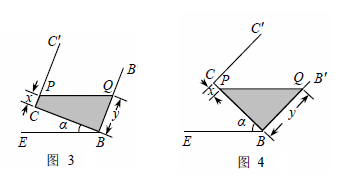
拓展:当容器向左旋转时,如图3,0°≤α≤37°,
∵液体体积不变,∴

。
∴y=-x+3.
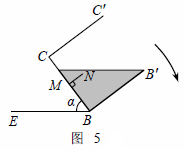
当容器向右旋转时,如图,同理可得:

。

当液面恰好到达容器口沿,即点Q与点B′重合时,如图,

由BB′=4,且

,得PB=3,
∴由tan∠PB′B=
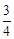
,得∠PB′B=37°。∴α=∠B′PB=53°。
此时37°≤α≤53°。
延伸:当α=60°时,如图所示,设FN∥EB,GB′∥EB,过点G作GH⊥BB′于点H。

在Rt△B′GH中,GH=MB=2,∠GB′B=30°,
∴HB′=2

。
∴MG=BH=4-2

<MN。
此时容器内液体形成两层液面,液体的形状分别是以Rt△NFM和直角梯形MBB′G为底面的直棱柱。
∵

,
∴

。
∴溢出液体可以达到4dm
3
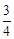 ,tan37°=
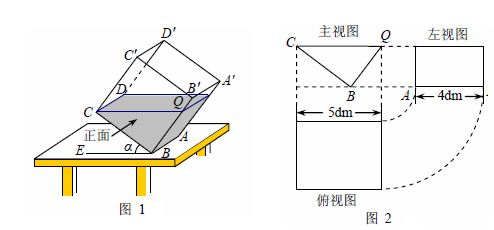
,tan37°=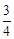 )
)
 。
。 。
。 。
。 ,∴α=∠BCQ=37°。
,∴α=∠BCQ=37°。 。
。 。
。

 ,得PB=3,
,得PB=3,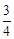 ,得∠PB′B=37°。∴α=∠B′PB=53°。
,得∠PB′B=37°。∴α=∠B′PB=53°。
 。
。 <MN。
<MN。 ,
, 。
。
