
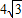 .四边形ABCD是菱形,点A在边PQ上,B、C在边QO上(B点在C点的左侧),且∠ABC=60°.设BQ=x.
.四边形ABCD是菱形,点A在边PQ上,B、C在边QO上(B点在C点的左侧),且∠ABC=60°.设BQ=x.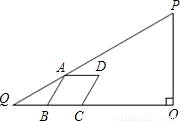
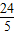 时,y=x×
时,y=x×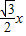 =
=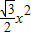 ,进而代入数据分析可得答案;
,进而代入数据分析可得答案;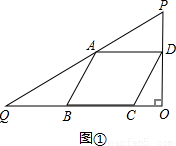 解:(1)∵∠Q=30°,∠ABC=60°,∴∠QAB=∠Q=30°.
解:(1)∵∠Q=30°,∠ABC=60°,∴∠QAB=∠Q=30°.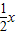 ,
,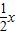
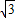 ,
,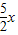 =12
=12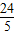 ;(2分)
;(2分)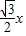
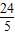 时,
时,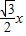 =
=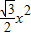 (2分)
(2分)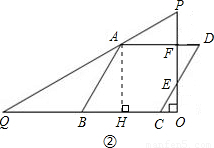
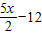 ,EF=
,EF= ?
?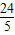 <x≤6时?,
<x≤6时?,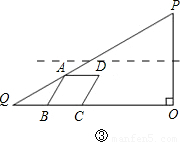 y=
y=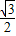 x2-
x2-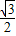 (
(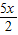 -12)2=-
-12)2=-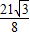 x2+30
x2+30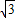 x-72
x-72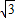 ;
;

科目:初中数学 来源: 题型:
| 3 |
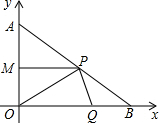
 PQ上,B、C在边QO上(B点在C点的左侧),且∠ABC=60°.设BQ=x.
PQ上,B、C在边QO上(B点在C点的左侧),且∠ABC=60°.设BQ=x.查看答案和解析>>
科目:初中数学 来源: 题型:
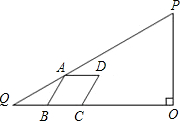
 分别为AB、OB边上的动点它们同时分别从点A、O向B点匀速运动,速度均为1cm/秒,设P、Q移动时间为t(0≤t≤4)
分别为AB、OB边上的动点它们同时分别从点A、O向B点匀速运动,速度均为1cm/秒,设P、Q移动时间为t(0≤t≤4)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 .四边形ABCD是菱形,点A在边
.四边形ABCD是菱形,点A在边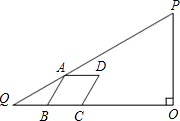 PQ上,B、C在边QO上(B点在C点的左侧),且∠ABC=60°.设BQ=x.
PQ上,B、C在边QO上(B点在C点的左侧),且∠ABC=60°.设BQ=x.查看答案和解析>>
科目:初中数学 来源:2009年浙江省嘉兴市桐乡市省一级重点高中招收保送生考试数学试卷(解析版) 题型:解答题
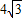 .四边形ABCD是菱形,点A在边PQ上,B、C在边QO上(B点在C点的左侧),且∠ABC=60°.设BQ=x.
.四边形ABCD是菱形,点A在边PQ上,B、C在边QO上(B点在C点的左侧),且∠ABC=60°.设BQ=x.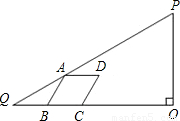
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com