
分析 (1)首先方程的两边同乘以最简公分母(x+3)(x-3),把分式方程转化为整式方程,再求解即可,最后要把求得的x的值代入到最简公分母进行检验.
(2)首先方程的两边同乘以最简公分母(x+1)(x-1),把分式方程转化为整式方程,再求解即可,最后要把求得的x的值代入到最简公分母进行检验.
解答 解:(1)方程两边同乘以最简公分母(x+3)(x-3)得:
x-3+2(x+3)=12,
解得:x=3,
检验:把x=3代入(x+3)(x-3)得:(3+3)×(3-3)=0,
故原方程无解.
(2)方程两边同乘以最简公分母(x+1)(x-1)得:
x(x+1)-3=(x+1)(x-1),
解得:x=2,
检验:把x=2代入(x+1)(x-1)得(2+1)×(2-1))≠0,
故原方程的解为x=2.
点评 本题主要考查解分式方程,关键在于“转化思想”,把分式方程转化为整式方程求解,最后一定注意要验根.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:选择题
| A. | x+1=x(1+$\frac{1}{x}$) | B. | x2-4+4x=(x+2)(x-2)+4x | ||
| C. | (x+3)(x-3)=x2-9 | D. | x2-2x-3=(x-3)(x+1) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
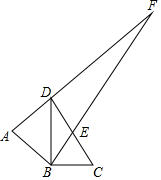 如图,△ABD是以BD为斜边的等腰直角三角形,△BCD中,∠DBC=90°,∠BCD=60°,DC中点为E,AD与BE的延长线交于点F,则∠AFB的度数为( )
如图,△ABD是以BD为斜边的等腰直角三角形,△BCD中,∠DBC=90°,∠BCD=60°,DC中点为E,AD与BE的延长线交于点F,则∠AFB的度数为( )| A. | 30° | B. | 15° | C. | 45° | D. | 25° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
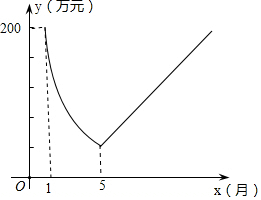 “保护生态环境,建设绿色社会”已经从理念变为人们的行动,某化工厂2016年1月的利润为200万元.设2016年1月为第1个月,第x个月的利润为y万元.由于排污超标,该厂决定从2016年1月底起适当限产,并投入资金进行治污改造,导致月利润明显下降,从1月到5月,y与x成反比例.到5月底,治污改造工程顺利完工,从这时起,该厂每月的利润比前一个月增加20万元(如图).
“保护生态环境,建设绿色社会”已经从理念变为人们的行动,某化工厂2016年1月的利润为200万元.设2016年1月为第1个月,第x个月的利润为y万元.由于排污超标,该厂决定从2016年1月底起适当限产,并投入资金进行治污改造,导致月利润明显下降,从1月到5月,y与x成反比例.到5月底,治污改造工程顺利完工,从这时起,该厂每月的利润比前一个月增加20万元(如图).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ②③④ | B. | ①②④ | C. | ③④ | D. | ②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
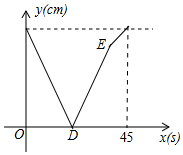 甲、乙两动点分别从线段AB的两端点同时出发,甲从点A出发,向终点B运动,乙从点B出发,向终点A运动.已知线段AB长为90cm,甲的速度为2.5cm/s.设运动时间为x(s),甲、乙两点之间的距离为y(cm),y与x的函数图象如图所示,则图中线段DE所表示的函数关系式为y=4.5x-90(20≤x≤36).(并写出自变量取值范围)
甲、乙两动点分别从线段AB的两端点同时出发,甲从点A出发,向终点B运动,乙从点B出发,向终点A运动.已知线段AB长为90cm,甲的速度为2.5cm/s.设运动时间为x(s),甲、乙两点之间的距离为y(cm),y与x的函数图象如图所示,则图中线段DE所表示的函数关系式为y=4.5x-90(20≤x≤36).(并写出自变量取值范围)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com