
分析 首先根据路程÷速度=时间,分别求出点P沿着长方形的边从A向B需要的时间,以及点P沿着长方形的边从B向C需要的时间各是多少;然后分两种情况:(1)点P在AB边上;(2)点P在BC边上;根据三角形的面积的求法,分类讨论,求出△APC的面积S与时间t之间的函数关系式,并指出自变量的取值范围即可.
解答 解:(1)如图1, ,
,
20÷2=10(s),
因为△APC的底AP=2t,高是10cm,
所以S=2t×10÷2=10t(0<t≤10);
(2)如图2,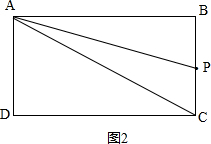 ,
,
10÷2=5(s),10+5=15(s),
因为△APC的底CP=(2t-20),高是20cm,
所以S=(2t-20)×20÷2=20t-200(10<t<15);
综上,可得S=$\left\{\begin{array}{l}{10t(0<t≤10)}\\{20t-200(10<t<15)}\end{array}\right.$.
点评 (1)此题主要考查了函数关系式的求法,以及函数的自变量的取值范围的确定,考查了分类讨论思想的应用,要熟练掌握;
(2)此题还考查了三角形的面积的求法,以及行程问题中速度、时间和路程的关系:速度×时间=路程,路程÷时间=速度,路程÷速度=时间,要熟练掌握.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,?ABCD的对角线AC、BD相交于点0,EF过点O与AD、BC分别相交于点E、F,若AB=5,AD=8,OE=3,那么四边形EFCD的周长为19.
如图,?ABCD的对角线AC、BD相交于点0,EF过点O与AD、BC分别相交于点E、F,若AB=5,AD=8,OE=3,那么四边形EFCD的周长为19.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
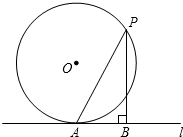 如图,直线l与半径为3的⊙O相切于点A,P是⊙O上的一个动点(不与点A重合),过点P作PB⊥l,垂足为B,连结PA,设PA=m,PB=n,则m-n的最大值是( )
如图,直线l与半径为3的⊙O相切于点A,P是⊙O上的一个动点(不与点A重合),过点P作PB⊥l,垂足为B,连结PA,设PA=m,PB=n,则m-n的最大值是( )| A. | 3 | B. | 2 | C. | $\frac{3}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
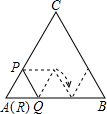 如图,正△ABC的边长为9cm,边长为3cm的正△RPQ的顶点R与点A重合,点P,Q分别在AC,AB上,将△RPQ沿着边AB,BC,CA连续翻转(如图所示),直至点P第一次回到原来的位置,则点P运动路径的长为6πcm.(结果保留π)
如图,正△ABC的边长为9cm,边长为3cm的正△RPQ的顶点R与点A重合,点P,Q分别在AC,AB上,将△RPQ沿着边AB,BC,CA连续翻转(如图所示),直至点P第一次回到原来的位置,则点P运动路径的长为6πcm.(结果保留π)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com